题目内容
（2013•济南一模）函数y=x-x
的图象大致为（ ）
| 1 |
| 3 |
分析：利用y=x-x
为奇函数可排除C，D，再利用x＞1时，y=x-x
＞0再排除一个，即可得答案．
| 1 |
| 3 |
| 1 |
| 3 |
解答：解：令y=f（x）=x-x
，
∵f（-x）=-x+x
=-（x-x
）=-f（x），
∴y=f（x）=x-x
为奇函数，
∴其图象关于原点成中心对称，故可排除C，D；
又x=1时，y=1-1=0，
当x＞1时，不妨令x=8，y=8-8
=6＞0，可排除B，
故选A．
| 1 |
| 3 |
∵f（-x）=-x+x
| 1 |
| 3 |
| 1 |
| 3 |
∴y=f（x）=x-x
| 1 |
| 3 |
∴其图象关于原点成中心对称，故可排除C，D；
又x=1时，y=1-1=0，
当x＞1时，不妨令x=8，y=8-8
| 1 |
| 3 |
故选A．
点评：本题考查函数的图象，着重考查函数的奇偶性与单调性，考查识图能力，属于中档题．
练习册系列答案
相关题目
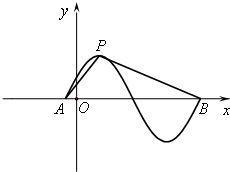（2013•济南一模）函数y=sin（