题目内容
对于R上可导的任意函数f(x),若满足(x+1)f′(x)≥0,则有( )
| A.f(0)+f(-2)<2f(-1) | B.f(0)+f(-2)≤2f(-1) |
| C.f(0)+f(-2)>2f(-1) | D.f(0)+f(-2)≥2f(-1) |
A
解析

练习册系列答案
相关题目
若函数 在
在 处有极值,则函数
处有极值,则函数 的图象在
的图象在 处的切线的斜率为( )
处的切线的斜率为( )
A. | B. | C. | D. |
若函数 的导函数是
的导函数是 ,则函数
,则函数

的单调递减区间是
A. | B. , , |
C. | D. , , |
曲线 在点
在点 处的切线方程为
处的切线方程为
A. | B. | C. | D. |
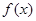 与
与 是定义在R上的两个可导函数,若
是定义在R上的两个可导函数,若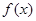 ,
, 满足
满足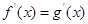 ,则
,则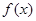 与
与 满足( )
满足( )
A.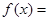  | B.  为常数函数 为常数函数 |
C.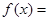 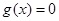 | D.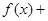  为常数函数 为常数函数 |
已知函数 的定义域为
的定义域为 ,部分对应值如下表,
,部分对应值如下表,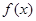 的导函数
的导函数 的图像如图所示.下列命题中,真命题的个数为 ( ).
的图像如图所示.下列命题中,真命题的个数为 ( ). 第12题图
第12题图 
① 函数 是周期函数;② 函数
是周期函数;② 函数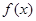 在
在 是减函数;③ 如果当
是减函数;③ 如果当 时,
时,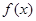 的最大值是
的最大值是 ,那么
,那么 的最大值为
的最大值为 ;④ 当
;④ 当 时,函数
时,函数 有
有 个零点,其中真命题的个数是 ( )
个零点,其中真命题的个数是 ( )
A. 个 个 | B. 个 个 | C. 个 个 | D. 个 个 |
曲线 在点
在点 处的切线的斜率为( )
处的切线的斜率为( )
A. | B. | C. | D. |
式子 的值是
的值是
A. | B.3 | C. | D.8 |
 的图象如右图所示,那么导函数
的图象如右图所示,那么导函数 的图象可能是( )
的图象可能是( )
