题目内容
附加题：设A、B是抛物线C：y2=2px（P＞0）上异于原点O的两个不同点，直线OA和OB的倾斜角分别为α和β，当α，β变化且α+β为定值θ（0＜θ＜π）时，证明直线AB恒过定点，并求出该定点的坐标．
（注：实验班必做，普通班选做）
分析：把OA的方程y=tanα•x，代入抛物线C：y2=2px，求得A的坐标，同理求得B的坐标，用两点式求得AB的方程，利用
α+β为定值θ 化简为 y=
（x+2p）-
x，可得过定点（-2p，
）．
α+β为定值θ 化简为 y=
| 1 |
| tanα+tanβ |
| 1 |
| tanθ |
| 2p |
| tanθ |
解答：解：OA的方程为 y=tanα•x，代入抛物线C：y2=2px，解得A（
，
），同理求得B（
，
），
用两点式求得AB的方程为
=
，化简可得 y=
x+
，
∵α+β为定值θ，∴tanθ=
，∴tanα•tanβ=
，
故直线AB的方程为 y=
x+
-
x=
（x+2p）-
x．
故x=-2p 时，y=
，故 直线AB过定点（-2p，
）．
| 2p |
| tan2α |
| 2p |
| tanα |
| 2p |
| tan2β |
| 2p |
| tanβ |
用两点式求得AB的方程为
y-
| ||||
|
x-
| ||||
|
| tanα•tanβ |
| tanα + tanβ |
| 2p |
| tanα + tanβ |
∵α+β为定值θ，∴tanθ=
| tanα+tanβ |
| 1-tanα•tanβ |
| tanθ- (tanα+tanβ) |
| tanθ |
故直线AB的方程为 y=
| 1 |
| tanα+tanβ |
| 2p |
| tanaα+ tnβ |
| 1 |
| tanθ |
| 1 |
| tanα+tanβ |
| 1 |
| tanθ |
故x=-2p 时，y=
| 2p |
| tanθ |
| 2p |
| tanθ |
点评：本题考查直线和圆的位置关系，直线过定点问题，化简直线AB的方程为 y=
（x+2p）-
x，
是解题的关键和难点．
| 1 |
| tanα+tanβ |
| 1 |
| tanθ |
是解题的关键和难点．
练习册系列答案
相关题目
)为方向向量的直线l过点(0, 
(p>0)的顶点关于直线l的对称点在该抛物的准线上．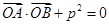
(O为原点，A、B异于原点)，试求点N的轨迹方程．