题目内容
(1)已知函数f(2x)=x2+x,求函数f(x)和f(x+1)的解析式.
(2)讨论函数f(x)=x+ 在[2,+∞)上的单调性.
在[2,+∞)上的单调性.
解:(1)令:2x=t,
则有x= t,
t,
∴f(t)= t2+
t2+ t
t
∴f(x)= x2+
x2+ x
x
f(x+1)= (x+1)2+
(x+1)2+ (x+1)=
(x+1)= x2+x+
x2+x+ ;
;
(2)由于x∈[2,+∞),则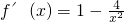 ≥0恒成立
≥0恒成立
故函数f(x)=x+ 在[2,+∞)上的单调递增.
在[2,+∞)上的单调递增.
分析:(1)用换元法求解,令:2x=t,则有x= t,可求得f(t),再令t=x,可求得f(x),最后求得f(x+1)的解析式;
t,可求得f(t),再令t=x,可求得f(x),最后求得f(x+1)的解析式;
(2)利用导数得到函数在[2,+∞)上的单调性.
点评:本题主要考查求函数解析式,常用方法有待定系数法,配方法,换元法,代换法,方程法等.
则有x=
 t,
t,∴f(t)=
 t2+
t2+ t
t∴f(x)=
 x2+
x2+ x
xf(x+1)=
 (x+1)2+
(x+1)2+ (x+1)=
(x+1)= x2+x+
x2+x+ ;
;(2)由于x∈[2,+∞),则
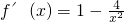 ≥0恒成立
≥0恒成立故函数f(x)=x+
 在[2,+∞)上的单调递增.
在[2,+∞)上的单调递增.分析:(1)用换元法求解,令:2x=t,则有x=
 t,可求得f(t),再令t=x,可求得f(x),最后求得f(x+1)的解析式;
t,可求得f(t),再令t=x,可求得f(x),最后求得f(x+1)的解析式;(2)利用导数得到函数在[2,+∞)上的单调性.
点评:本题主要考查求函数解析式,常用方法有待定系数法,配方法,换元法,代换法,方程法等.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目