题目内容
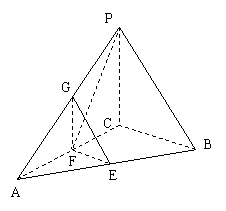 三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.
三棱锥P-ABC中,PC、AC、BC两两垂直,BC=PC=1,AC=2,E、F、G分别是AB、AC、AP的中点.
(Ⅰ)证明平面GFE∥平面PCB;
(Ⅱ)求二面角B-AP-C的余弦;
(Ⅲ)求直线PF与平面PAB所成角的正弦.
(Ⅰ)证明:因为E、F、G分别是AB、AC、AP的中点,
所以EF∥BC,GF∥CP. …………………………………………………1分
因为EF、GF![]() 平面PCB,
平面PCB,
所以EF∥平面PCB,GF∥平面PCB.
又EF∩GF= F,
所以平面GFE∥平面PCB. …………………………………3分
依条件建立如图所示空间直角坐标系C-xyz.
所以A(2,0,0),B(0,1,0), P(0,0,1)
(Ⅱ)解:显然![]() =(0,1,0)是平面PAC的一个法向量.
=(0,1,0)是平面PAC的一个法向量.
设n=(x,y,z)是平面PAB的一个法向量,
因为![]() =(-2,0,1),
=(-2,0,1),![]() =(-2,1,0),
=(-2,1,0),
所以由n·![]() =0,n·
=0,n·![]() =0解得n=(1,2,2). …………………………6分
=0解得n=(1,2,2). …………………………6分
设二面角B-AP-C的大小为![]() ,
,
所以cos![]() =
=![]() =
=![]() .
.
所以二面角B-AP-C的余弦为![]() . …………8分
. …………8分
(Ⅲ)解:设PF与平面PAB所成的角为![]() ,
,
由(Ⅱ)知平面PAB的一个法向量n=(1,2,2).
又![]() =(-1,0, 1),所以cos(
=(-1,0, 1),所以cos(![]() -
-![]() )=
)=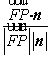 =
=![]() . ……11分
. ……11分
所以sin![]() =
=![]() .即直线AC与平面PAB所成角的正弦是
.即直线AC与平面PAB所成角的正弦是![]() .……………13分
.……………13分

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
 如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.
如图,在三棱锥P-ABC中,△PAB是等边三角形,∠PAC=∠PBC=90°.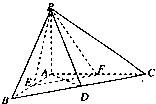 如图,在三棱锥P-ABC中,
如图,在三棱锥P-ABC中,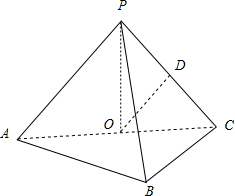 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.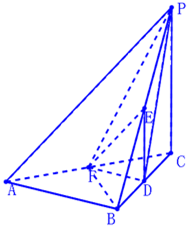 如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.
如图,在三棱锥P-ABC中,PC⊥平面ABC,△ABC为正三角形,D、E、F分别是BC,PB,CA的中点.