题目内容
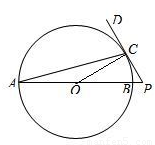
如图,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.已知圆O半径为 ,OP=2,则PC= ;∠ACD的大小为 .
,OP=2,则PC= ;∠ACD的大小为 .
【答案】分析:连接OC,AB是圆O的直径,P在AB的延长线上,PD切圆O于点C.圆O半径为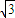 ,OP=2,所以PB=2-
,OP=2,所以PB=2-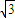 ,PA=2+
,PA=2+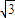 ,PC2=PB•PA=1,PC=1.在Rt△OCP中,由∠OCP=90°,PC=1,OP=2,知∠COP=30°,由此能求出∠ACD的大小.
,PC2=PB•PA=1,PC=1.在Rt△OCP中,由∠OCP=90°,PC=1,OP=2,知∠COP=30°,由此能求出∠ACD的大小.
解答:解:连接OC,
∵AB是圆O的直径,P在AB的延长线上,
PD切圆O于点C.圆O半径为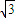 ,OP=2,
,OP=2,
∴PB=2-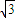 ,PA=2+
,PA=2+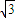 ,
,
∴PC2=PB•PA
=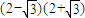 =1,
=1,
∴PC=1.
在Rt△OCP中,
∵∠OCP=90°,PC=1,OP=2,
∴∠COP=30°,
∴∠OCA=15°,
∴∠ACD=90°-15°=75°.
故答案为:1,75°.
点评:本题考查圆的切割线定理的应用,是基础题.解题时要认真审题,仔细解答,注意与圆有关的比例线段的灵活运用.
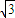 ,OP=2,所以PB=2-
,OP=2,所以PB=2-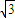 ,PA=2+
,PA=2+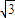 ,PC2=PB•PA=1,PC=1.在Rt△OCP中,由∠OCP=90°,PC=1,OP=2,知∠COP=30°,由此能求出∠ACD的大小.
,PC2=PB•PA=1,PC=1.在Rt△OCP中,由∠OCP=90°,PC=1,OP=2,知∠COP=30°,由此能求出∠ACD的大小.解答:解:连接OC,
∵AB是圆O的直径,P在AB的延长线上,
PD切圆O于点C.圆O半径为
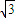 ,OP=2,
,OP=2,∴PB=2-
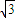 ,PA=2+
,PA=2+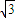 ,
,∴PC2=PB•PA
=
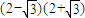 =1,
=1,∴PC=1.
在Rt△OCP中,
∵∠OCP=90°,PC=1,OP=2,
∴∠COP=30°,
∴∠OCA=15°,
∴∠ACD=90°-15°=75°.
故答案为:1,75°.

点评:本题考查圆的切割线定理的应用,是基础题.解题时要认真审题,仔细解答,注意与圆有关的比例线段的灵活运用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目


 如图,直三棱柱的一个底面ABC内接于圆O,AB是圆O的直径.
如图,直三棱柱的一个底面ABC内接于圆O,AB是圆O的直径.



 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数