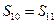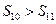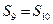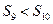题目内容
(本题满分14分)已知函数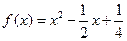 ,
,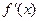 为函数
为函数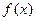 的导函数.
的导函数.
(Ⅰ)若数列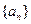 满足:
满足: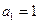 ,
,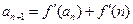 (
(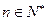 ),求数列
),求数列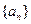 的通项
的通项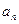 ;
;
(Ⅱ)若数列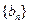 满足:
满足: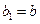 ,
,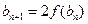 (
(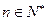 ).
).
ⅰ.当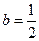 时,数列
时,数列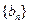 是否为等差数列?若是,请求出数列
是否为等差数列?若是,请求出数列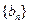 的通项
的通项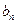 ;若不是,请说明理由;
;若不是,请说明理由;
ⅱ.当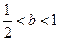 时, 求证:
时, 求证: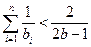 .
.
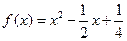 ,
,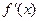 为函数
为函数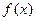 的导函数.
的导函数.(Ⅰ)若数列
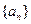 满足:
满足: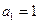 ,
,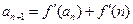 (
(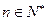 ),求数列
),求数列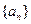 的通项
的通项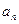 ;
;(Ⅱ)若数列
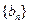 满足:
满足: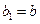 ,
,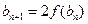 (
(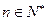 ).
).ⅰ.当
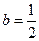 时,数列
时,数列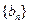 是否为等差数列?若是,请求出数列
是否为等差数列?若是,请求出数列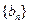 的通项
的通项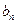 ;若不是,请说明理由;
;若不是,请说明理由;ⅱ.当
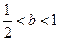 时, 求证:
时, 求证: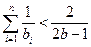 .
.(Ⅰ)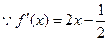 , …………………1分
, …………………1分
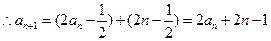 ,
,
即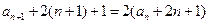 . …………………………3分
. …………………………3分
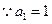 ,
, 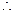 数列
数列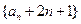 是首项为
是首项为 ,公比为
,公比为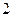 的等比数列.
的等比数列.
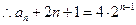 ,即
,即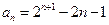 . …………………………5分
. …………………………5分
(Ⅱ)(ⅰ)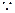
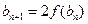
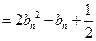 ,
,
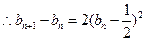 .
.
 当
当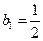 时,
时,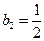 .
.
假设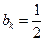 ,则
,则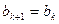 .
.
由数学归纳法,得出数列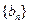 为常数数列,是等差数列,其通项为
为常数数列,是等差数列,其通项为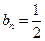 . …………8分
. …………8分
(ⅱ)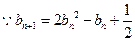 ,
, 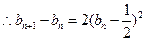 .
.
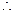 当
当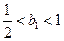 时,
时,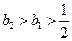 .
.
假设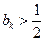 ,则
,则 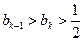 .
.
由数学归纳法,得出数列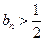
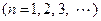 . …………………………10分
. …………………………10分
又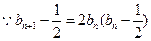 ,
,
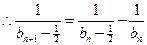 ,
,
即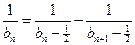 . …………………………12分
. …………………………12分
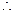
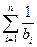
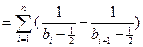
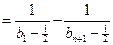 .
.
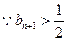 ,
,
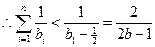 . …………………………14分
. …………………………14分
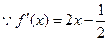 , …………………1分
, …………………1分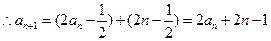 ,
,即
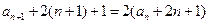 . …………………………3分
. …………………………3分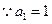 ,
, 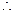 数列
数列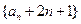 是首项为
是首项为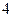 ,公比为
,公比为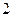 的等比数列.
的等比数列.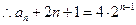 ,即
,即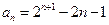 . …………………………5分
. …………………………5分(Ⅱ)(ⅰ)
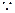
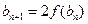
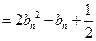 ,
,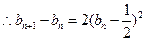 .
.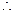 当
当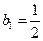 时,
时,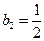 .
.假设
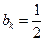 ,则
,则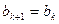 .
.由数学归纳法,得出数列
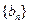 为常数数列,是等差数列,其通项为
为常数数列,是等差数列,其通项为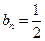 . …………8分
. …………8分(ⅱ)
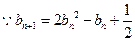 ,
, 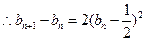 .
.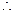 当
当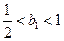 时,
时,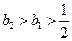 .
.假设
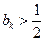 ,则
,则 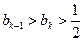 .
.由数学归纳法,得出数列
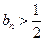
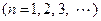 . …………………………10分
. …………………………10分又
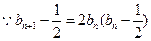 ,
,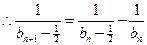 ,
,即
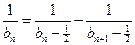 . …………………………12分
. …………………………12分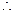
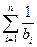
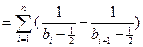
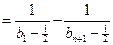 .
.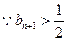 ,
,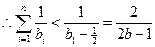 . …………………………14分
. …………………………14分同答案

练习册系列答案
相关题目
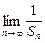 ,其中Sn=b1+b2+…+bn;
,其中Sn=b1+b2+…+bn;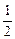 ,求数列{
,求数列{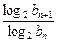 }的最大项和最小项的值.
}的最大项和最小项的值. 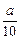 )x(0<a<1)的图像上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形.
)x(0<a<1)的图像上,且点Pn,点(n,0)与点(n+1,0)构成一个以Pn为顶点的等腰三角形. 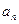 }的前n项和为
}的前n项和为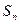 ,若
,若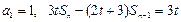 (t为正常数,n=2,3,4…).
(t为正常数,n=2,3,4…).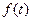 ,作数列
,作数列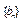 使
使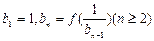 ,试求
,试求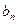 ,并求
,并求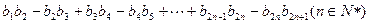
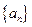 的前
的前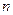 项和为
项和为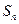 ,且
,且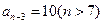 ,
,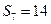 ,
,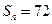 ,则
,则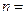 .
.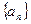 中,
中,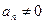 ,且
,且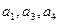 成等比数列,则其公比
成等比数列,则其公比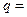 .
.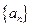 是等差数列,且
是等差数列,且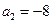 ,
,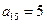 ,
,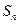 是数列
是数列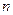 项和,则
项和,则