题目内容
已知直线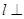 平面
平面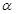 ,直线
,直线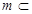 平面
平面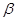 ,则下列四个命题中正确的是 ( )
,则下列四个命题中正确的是 ( )
①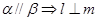 ②
②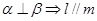 ;③
;③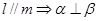 ;④
;④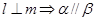
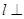 平面
平面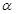 ,直线
,直线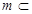 平面
平面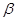 ,则下列四个命题中正确的是 ( )
,则下列四个命题中正确的是 ( )①
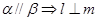 ②
②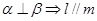 ;③
;③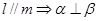 ;④
;④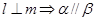
| A.②④ | B.①② | C.③④ | D.①③ |
D
① ,又因为
,又因为 ,所以
,所以 ,又因为
,又因为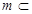 平面
平面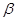 ,所以
,所以 .正确.
.正确.
③ ,又因为
,又因为 ,所以
,所以 .正确.
.正确.
 ,又因为
,又因为 ,所以
,所以 ,又因为
,又因为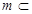 平面
平面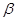 ,所以
,所以 .正确.
.正确.③
 ,又因为
,又因为 ,所以
,所以 .正确.
.正确.
练习册系列答案
相关题目
题目内容
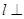 平面
平面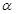 ,直线
,直线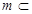 平面
平面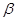 ,则下列四个命题中正确的是 ( )
,则下列四个命题中正确的是 ( )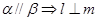 ②
②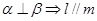 ;③
;③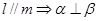 ;④
;④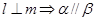
| A.②④ | B.①② | C.③④ | D.①③ |
 ,又因为
,又因为 ,所以
,所以 ,又因为
,又因为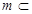 平面
平面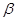 ,所以
,所以 .正确.
.正确. ,又因为
,又因为 ,所以
,所以 .正确.
.正确.