题目内容
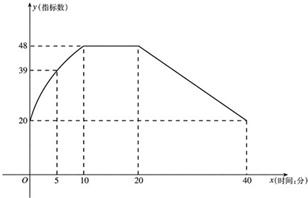 通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散.学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.
通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散.学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.(1)当0≤x≤10时,求注意力指标数y与时间x的函数关系式;
(2)一道数学竞赛题需要讲解24分钟.问老师能否经过适当安排,使学生在听这道题时,注意力的指标数都不低于36.
分析:(1)由已知我们易得函数的类型,故可以利用待定系数法解答本题,由函数的图象设出函数的解析式,将图象上的点代入后易构造出一个关于a,b,c的方程组,解方程组求出a,b,c的值,即可求出函数注意力指标数y与时间x的函数关系式;
(2)根据(1)中的函数解析式,我们可以求出学生在听这道题时,注意力的指标数都不低于36的x的值,然后和24进行比较,即可得到结论.
(2)根据(1)中的函数解析式,我们可以求出学生在听这道题时,注意力的指标数都不低于36的x的值,然后和24进行比较,即可得到结论.
解答:解:(1)当0≤x≤10时,设抛物线的函数关系式为y=ax2+bx+c,
由于它的图象经过点(0,20),(5,39),(10,48),
所以
解得,a=-
,b=
,c=20.
所以y=-
x2+
x+20,0≤x≤10.(6分)
(2)当20≤x≤40时,y=-
x+76.
所以,当0≤x≤10时,令y=36,
得36=-
x2+
x+20,
解得x=4,x=20(舍去);
当20≤x≤40时,令y=36,得36=-
x+76,
解得x=
=28
.(13分)
因为28
-4=24
>24,
所以,老师可以经过适当的安排,在学生注意力指标数不低于36时,讲授完这道竞赛题.
由于它的图象经过点(0,20),(5,39),(10,48),
所以
|
解得,a=-
| 1 |
| 5 |
| 24 |
| 5 |
所以y=-
| 1 |
| 5 |
| 24 |
| 5 |
(2)当20≤x≤40时,y=-
| 7 |
| 5 |
所以,当0≤x≤10时,令y=36,
得36=-
| 1 |
| 5 |
| 24 |
| 5 |
解得x=4,x=20(舍去);
当20≤x≤40时,令y=36,得36=-
| 7 |
| 5 |
解得x=
| 200 |
| 7 |
| 4 |
| 7 |
因为28
| 4 |
| 7 |
| 4 |
| 7 |
所以,老师可以经过适当的安排,在学生注意力指标数不低于36时,讲授完这道竞赛题.
点评:本题考查的知识点是函数的图象与图象的变化,其中根据已知中函数的图象,结合待定系数法,求出满足条件的函数的解析式是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
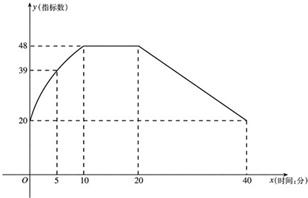 通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散.学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.
通过实验研究,专家们发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持平稳的状态,随后开始分散.学生注意力指标数y随时间x(分钟)变化的函数图象如图所示(y越大表示学生注意力越集中).当0≤x≤10时,图象是抛物线的一部分,当10≤x≤20和20≤x≤40时,图象是线段.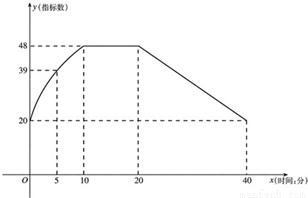
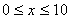 时,图象是抛物线的一部分,当
时,图象是抛物线的一部分,当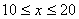 和
和 时,图象是线段.
时,图象是线段.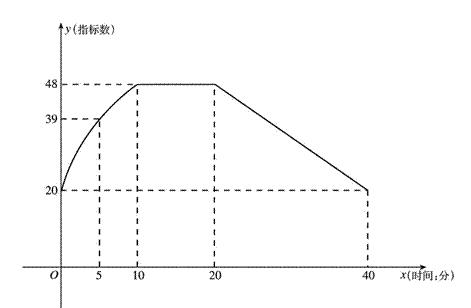 (2)一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排,使学生在听这道题时,注意力的指标数都不低于36.
(2)一道数学竞赛题需要讲解24分钟. 问老师能否经过适当安排,使学生在听这道题时,注意力的指标数都不低于36.