题目内容
(选做题)
已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x。
(Ⅰ)解关于x的不等式g(x)≥f(x)-|x-1|;
(Ⅱ)如果对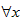 ∈R,不等式g(x)+c≤f(x)-|x-1|恒成立,求实数c的取值范围。
∈R,不等式g(x)+c≤f(x)-|x-1|恒成立,求实数c的取值范围。
已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x。
(Ⅰ)解关于x的不等式g(x)≥f(x)-|x-1|;
(Ⅱ)如果对
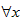 ∈R,不等式g(x)+c≤f(x)-|x-1|恒成立,求实数c的取值范围。
∈R,不等式g(x)+c≤f(x)-|x-1|恒成立,求实数c的取值范围。解:(Ⅰ)∵函数f(x)和g(x)的图象关于原点对称,
∴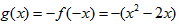 ,
,
∴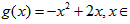 R,
R,
∴原不等式可化为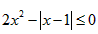 ,
,
上面不等价于下列二个不等式组: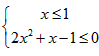 ……①,
……①,
或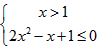 ……②,
……②,
由①得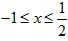 ,而②无解,
,而②无解,
∴原不等式的解集为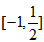 ;
;
(Ⅱ)不等式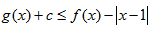 可化为:
可化为: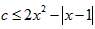 ,
,
作出函数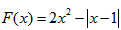 的图象(这里略),
的图象(这里略),
由此可得函数F(x)的最小值为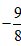 ,
,
∴实数c的取值范围是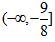 。
。
∴
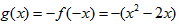 ,
, ∴
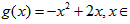 R,
R,∴原不等式可化为
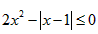 ,
,上面不等价于下列二个不等式组:
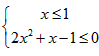 ……①,
……①,或
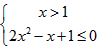 ……②,
……②,由①得
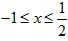 ,而②无解,
,而②无解,∴原不等式的解集为
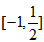 ;
;(Ⅱ)不等式
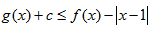 可化为:
可化为: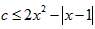 ,
,作出函数
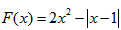 的图象(这里略),
的图象(这里略),由此可得函数F(x)的最小值为
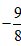 ,
,∴实数c的取值范围是
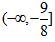 。
。 
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目