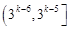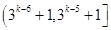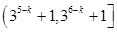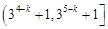题目内容
已知对任意实数 ,有
,有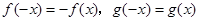 ,且
,且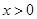 时,
时,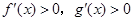 ,则
,则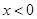 时( )
时( )
A.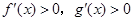 | B.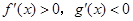 |
C. | D.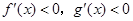 |
B
解析试题分析:解:∵对任意实数x,有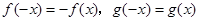 ,∴函数f(x)是奇函数,g(x)是偶函数.我们知道:奇函数的图象关于原点对称,其单调性在x>0与x<0时相同;偶函数的图象关于y轴对称,其单调性在x>0与x<0时相反;又∵当x>0时,
,∴函数f(x)是奇函数,g(x)是偶函数.我们知道:奇函数的图象关于原点对称,其单调性在x>0与x<0时相同;偶函数的图象关于y轴对称,其单调性在x>0与x<0时相反;又∵当x>0时,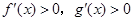 ,∴当x<0时,
,∴当x<0时,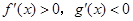 ,故选B.
,故选B.
考点:函数的奇偶性
点评:正确理解函数的奇偶性和如何利用导数研究函数的单调性是解题的关键.

练习册系列答案
相关题目
偶函数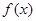 满足
满足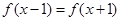 ,当
,当 时,
时, 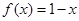 ,则关于
,则关于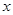 的方程
的方程 在
在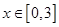 上解的个数是( )
上解的个数是( )
| A.1 | B.2 | C.3 | D.4 |
已知函数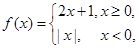 且
且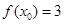 ,则实数
,则实数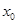 的值为( )
的值为( )
A.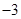 | B.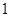 | C.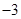 或 或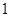 | D.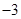 或 或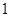 或 或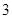 |
函数f(x)=ln(4+3x-x2)的单调递减区间是
A.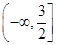 | B.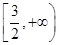 | C.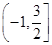 | D.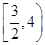 |
函数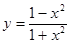 的值域是( )
的值域是( )
| A.[-1,1] | B.(-1,1] | C.[-1,1) | D.(-1,1) |
函数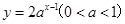 的图象一定过点( )
的图象一定过点( )
| A.(1,1) | B.(1,2) | C.(2,0) | D.(2,-1) |
已知函数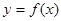 的导函数
的导函数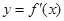 的图像如下,则( )
的图像如下,则( )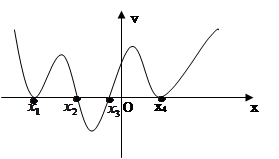
A.函数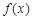 有1个极大值点,1个极小值点 有1个极大值点,1个极小值点 |
B.函数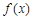 有2个极大值点,2个极小值点 有2个极大值点,2个极小值点 |
C.函数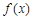 有3个极大值点,1个极小值点 有3个极大值点,1个极小值点 |
D.函数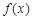 有1个极大值点,3个极小值点 有1个极大值点,3个极小值点 |
下列函数中,周期为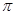 ,且在区间
,且在区间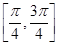 上单调递增的函数是
上单调递增的函数是
A.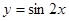 | B.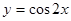 | C.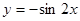 | D.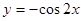 |
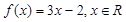 规定:给出一个实数
规定:给出一个实数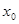 ,赋值
,赋值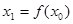 ,若
,若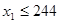 ,则继续赋值
,则继续赋值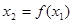 , ,
, , 以此类推,若
以此类推,若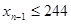 ,则
,则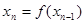 ,否则停止赋值,如果得到
,否则停止赋值,如果得到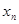 称为赋值了
称为赋值了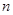 次
次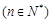 .已知赋值了
.已知赋值了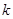 次后停止,则
次后停止,则