题目内容
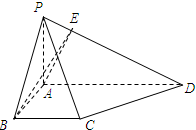 如图,在直角梯形ABCD外一点P,且∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角.AE⊥PD,E为垂足.
如图,在直角梯形ABCD外一点P,且∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角.AE⊥PD,E为垂足.(1)求点D到平面PBC的距离;
(2)求证:BE⊥PD;
(3)求异面直线AE与CD所成角的大小.(用反三角函数来表示)
分析:(1)以A为原点,AB,AD,AP所在直线为坐标轴建立直角坐标系,先求出平面PBC的法向量,然后求出CD向量在法向量上的投影的长度即为D点到平面PBC的距离.
(2)根据向量数量积为零可知线线垂直,从而
⊥面BEA,根据线面垂直的性质可知PD⊥BE.
(3)先分别求出向量
,向量
的坐标,然后利用空间向量的夹角公式求出两向量的夹角的余弦值,进而得到AE与CD所成角的余弦值,即可得到答案.
(2)根据向量数量积为零可知线线垂直,从而
| PD |
(3)先分别求出向量
| AE |
| CD |
解答:解:(1)为了计算方便不妨设a=1,所以AB=BC=1,AD=2,
由题意可得:以A为原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立直角坐标系(如图),
则 A(0,0,0),B(1,0,0)D(0,2,0)P(0,0,
),C(1,1,0),
所以
=(1,0,-
),
=(0,1,0),
=(-1,1,0),
设
=(x,y,z),并且
⊥平面PBC,则
⊥
,
⊥
,
所以
,即
,
令z=1则 x=
,
=(
,0, 1)
D点到平面PBC的距离设为d,
则 d=
=
,
即D点到平面PBC的距离为
,
所以D点到平面PBC的距离为
a.
(2)证明:由题意可得:
=(1,0,0),
=(0,2,-
),
所以
•
=(1,0,0)•(0,2,-
)=0,
所以
⊥
,即AB⊥PD,
又因为AE⊥PD,
所以 PD⊥面BEA,
又因为BE?面BEA,
所以PD⊥BE.
(3)∵PA⊥面ABCD,PD与底面成30°角,
∴∠PDA=30°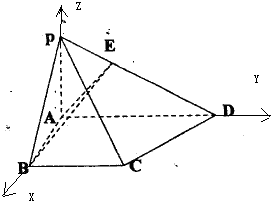
过E作EF⊥AD,垂足为F,则AE=AD•sin30°=1,并且∠EAF=60°
所以AF=
,EF=
∴E(0,
,
),
于是
=(0,
,
)
又 C(1,1,0),D(0,2,0),
=(-1,1,0)
则 COSθ=
=
,
所以AE与CD所成角的余弦值为
,
所以异面直线AE与CD所成角的大小为arccos
.
由题意可得:以A为原点,AB,AD,AP所在直线分别为x轴,y轴,z轴建立直角坐标系(如图),
则 A(0,0,0),B(1,0,0)D(0,2,0)P(0,0,
2
| ||
| 3 |
所以
| PB |
2
| ||
| 3 |
| BC |
| CD |
设
| V |
| V |
| V |
| BC |
| V |
| PB |
所以
|
|
令z=1则 x=
2
| ||
| 3 |
| V |
2
| ||
| 3 |
D点到平面PBC的距离设为d,
则 d=
|
| ||||
|
|
2
| ||
| 7 |
即D点到平面PBC的距离为
2
| ||
| 7 |
所以D点到平面PBC的距离为
2
| ||
| 7 |
(2)证明:由题意可得:
| AB |
| PD |
2
| ||
| 3 |
所以
| AB |
| PD |
2
| ||
| 3 |
所以
| AB |
| PD |
又因为AE⊥PD,
所以 PD⊥面BEA,
又因为BE?面BEA,
所以PD⊥BE.
(3)∵PA⊥面ABCD,PD与底面成30°角,
∴∠PDA=30°

过E作EF⊥AD,垂足为F,则AE=AD•sin30°=1,并且∠EAF=60°
所以AF=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
于是
| AE |
| 1 |
| 2 |
| ||
| 2 |
又 C(1,1,0),D(0,2,0),
| CD |
则 COSθ=
| ||||
|
|
| ||
| 4 |
所以AE与CD所成角的余弦值为
| ||
| 4 |
所以异面直线AE与CD所成角的大小为arccos
| ||
| 4 |
点评:本题主要考查了线线的位置关系、线线所成角以及点到面的距离,同时考查了利用空间向量求解立体几何问题,考查空间想象能力,运算求解能力,属于综合题.

练习册系列答案
相关题目
 如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD= 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD,
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=DC=PD=2.点E、F分别是PC、BD的中点,现将△PDC沿CD折起,使PD⊥平面ABCD, 如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设
如图,在直角梯形ABCD中,AB∥CD,AD=CD=1,AB=3,动点P在BCD内运动(含边界),设 如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则
如图,在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=4,BC=2,AD=4,若P为CD的中点,则