题目内容
如图，在三棱锥P-ABC中，已知PC⊥BC，PC⊥AC，点E，F，G分别是所在棱的中点，则下面结论中正确的是：①②③
①②③
．①平面EFG∥平面PBC
②平面EFG⊥平面ABC
③∠BPC是直线EF与直线PC所成的角
④∠FEG是平面PAB与平面ABC所成二面角的平面角．
分析：结合已知中PC⊥BC，PC⊥AC，点E，F，G分别是所在棱的中点，结合三角形的中位线定理和面面垂直的判定定理，可以判断①的真假；根据面面垂直的判定定理，可以判断②的真假；根据异面直线夹角的定义，可以判断③的真假，根据二面角的定义可以判断④的真假．
解答：解：由已知中E，F，G分别是所在棱的中点，
则EF∥PB，EG∥BC，由面面平行的判定定理可得①正确；
由PC⊥BC，PC⊥AC，结合线面垂直的判定定理可得PC⊥平面ABC，又由FC∥PC，则FC⊥平面ABC
再由面面垂直的判定定理，可得平面EFG⊥平面ABC，故②正确；
∵EF∥BP，故③∠BPC是直线EF与直线PC所成的角正确
∵FE与AB不垂直，GE与AB也不垂直，故④∠FEG不是平面PAB与平面ABC所成二面角的平面，即④错误；
故答案为：①②③
则EF∥PB，EG∥BC，由面面平行的判定定理可得①正确；
由PC⊥BC，PC⊥AC，结合线面垂直的判定定理可得PC⊥平面ABC，又由FC∥PC，则FC⊥平面ABC
再由面面垂直的判定定理，可得平面EFG⊥平面ABC，故②正确；
∵EF∥BP，故③∠BPC是直线EF与直线PC所成的角正确
∵FE与AB不垂直，GE与AB也不垂直，故④∠FEG不是平面PAB与平面ABC所成二面角的平面，即④错误；
故答案为：①②③
点评：本题考查的知识点是棱锥的结构特征，异面直线及其所成的角，直线与平面平行的判定，直线与平面垂直的判定，二面角的平面角及求法，熟练掌握空间直线与平面垂直及平行的判定定理及异面直线夹角和二面角的定义是解答本题的关键．
练习册系列答案
相关题目
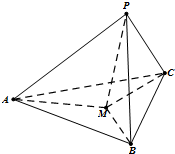如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3．PB=2，PC=1．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f（M）=（
如图，在三棱锥P-ABC中，PA⊥底面ABC，∠ACB=90°，AE⊥PB于E，AF⊥PC于F，若PA=AB=2，∠BPC=θ，则当△AEF的面积最大时，tanθ的值为（ ）
如图，在三棱锥P-ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D、E分别为AB、AC中点．
如图，在三棱锥P-ABC中，已知PA=PB=PC，∠BPA=∠BPC=∠CPA=40°，一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是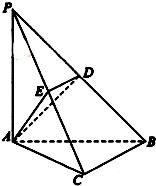
如图，在三棱锥P-ABC中，PA⊥底面ABC，∠BCA=90°，AP=AC，点D，E分别在棱