题目内容
给出下列命题：①
；②?x∈R，x2+1≤2x；③若x＞0，y＞0，则
．其中所有真命题的序号是________．
②③
分析：①令x=-1，可得
，从而进行判断；
②?x∈R，x2+1≤2x，对其进行移项，配方，再进行判断；
③根据均值不等式：
（a，b＞0）进行判断；
解答：①令x=-1，可得x+
=-1-1=-2≤2，故①错误；
②?x∈R，x2+1≤2x，∴（x-1）2≤0，令x=1，可得0≤0，故②正确；
③∵x＞0，y＞0，由已知均值不等式：（a，b＞0），
∴=
，故③正确
故答案为：②③；
点评：此题主要考查均值不等式的性质，注意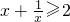
要求x，y＞0，不能忘记条件，这是同学们容易出错的地方，此题是一道基础题．
分析：①令x=-1，可得
，从而进行判断；②?x∈R，x2+1≤2x，对其进行移项，配方，再进行判断；
③根据均值不等式：
（a，b＞0）进行判断；解答：①令x=-1，可得x+
=-1-1=-2≤2，故①错误；②?x∈R，x2+1≤2x，∴（x-1）2≤0，令x=1，可得0≤0，故②正确；
③∵x＞0，y＞0，由已知均值不等式：
（a，b＞0），∴
=，故③正确故答案为：②③；
点评：此题主要考查均值不等式的性质，注意
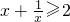要求x，y＞0，不能忘记条件，这是同学们容易出错的地方，此题是一道基础题． 
练习册系列答案
高中必刷题系列答案
相关题目