题目内容
已知f(x)=x2+2x+alnx(1)当a=-4,求f(x)的最小值;
(2)若f(x)在(0,1)不单调,求a的取值范围;
(3)当t≥1时,f(2t-1)≥2f(t)-3恒成立,求a的取值范围.
【答案】分析:(1)把a=4代入函数解析式,求导后得到导函数在定义域内的零点,由零点对定义域分段后判断导函数的符号,从而得到极小值点,求出极小值即最小值;
(2)求出函数的导函数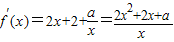 ,引入辅助函数g(x)=2x2+2x+a,因为x>0,要使f(x)在(0,1)不单调,则需g(x)在(0,1)内不同号,利用“三个二次”的结合得到关于a的不等式组,从而求出a的取值范围;
,引入辅助函数g(x)=2x2+2x+a,因为x>0,要使f(x)在(0,1)不单调,则需g(x)在(0,1)内不同号,利用“三个二次”的结合得到关于a的不等式组,从而求出a的取值范围;
(3)把不等式f(2t-1)≥2f(t)-3变形为2t2-alnt2≥2(2t-1)-aln(2t-1),构造辅助函数h(x)=2x-alnx(x≥1),问题转化为证明该函数为增函数,利用导数即可证明.
解答:解:(1)函数f(x)的定义域是(0,+∞)
当a=-4时,f(x)=x2+2x-4lnx,
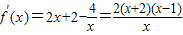 .
.
当x∈(0,1)时,f′(x)0.
所以,f(x)在x=1时取得极小值,也就是最小值,等于f(1)=3;
(2)因为f(x)=x2+2x+alnx(x>0),
所以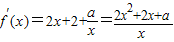 .
.
设g(x)=2x2+2x+a,
∵函数f(x)在区间(0,1)上不单调,
∴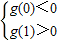 ,即
,即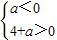 ,解得-4<a<0.
,解得-4<a<0.
∴实数a的取值范围是{a|-4<a<0};
(3)不等式f(2t-1)≥2f(t)-3可化为
2t2-4t+2≥alnt2-aln(2t-1)
∴2t2-alnt2≥2(2t-1)-aln(2t-1)
令h(x)=2x-alnx(x≥1),则问题可化为h(t2)≥h(2t-1)
∵t≥1,∴t2≥2t-1
要使上式成立,只需要h(x)=2x-alnx(x≥1)是增函数即可.
即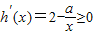 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,
即a≤2x在[1,+∞)上恒成立,
故a≤2.
∴实数a的取值范围是(-∞,2].
点评:本题考查了利用导数求闭区间上的最值,考查了数学转化思想方法,考查了函数构造法,该题(3)巧妙地转化构造函数,使该题解题过程变得较为简洁,起到了事半功倍的效果,该题是难题.
(2)求出函数的导函数
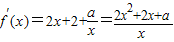 ,引入辅助函数g(x)=2x2+2x+a,因为x>0,要使f(x)在(0,1)不单调,则需g(x)在(0,1)内不同号,利用“三个二次”的结合得到关于a的不等式组,从而求出a的取值范围;
,引入辅助函数g(x)=2x2+2x+a,因为x>0,要使f(x)在(0,1)不单调,则需g(x)在(0,1)内不同号,利用“三个二次”的结合得到关于a的不等式组,从而求出a的取值范围;(3)把不等式f(2t-1)≥2f(t)-3变形为2t2-alnt2≥2(2t-1)-aln(2t-1),构造辅助函数h(x)=2x-alnx(x≥1),问题转化为证明该函数为增函数,利用导数即可证明.
解答:解:(1)函数f(x)的定义域是(0,+∞)
当a=-4时,f(x)=x2+2x-4lnx,
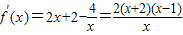 .
.当x∈(0,1)时,f′(x)0.
所以,f(x)在x=1时取得极小值,也就是最小值,等于f(1)=3;
(2)因为f(x)=x2+2x+alnx(x>0),
所以
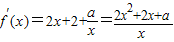 .
.设g(x)=2x2+2x+a,
∵函数f(x)在区间(0,1)上不单调,
∴
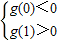 ,即
,即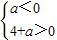 ,解得-4<a<0.
,解得-4<a<0.∴实数a的取值范围是{a|-4<a<0};
(3)不等式f(2t-1)≥2f(t)-3可化为
2t2-4t+2≥alnt2-aln(2t-1)
∴2t2-alnt2≥2(2t-1)-aln(2t-1)
令h(x)=2x-alnx(x≥1),则问题可化为h(t2)≥h(2t-1)
∵t≥1,∴t2≥2t-1
要使上式成立,只需要h(x)=2x-alnx(x≥1)是增函数即可.
即
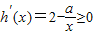 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,即a≤2x在[1,+∞)上恒成立,
故a≤2.
∴实数a的取值范围是(-∞,2].
点评:本题考查了利用导数求闭区间上的最值,考查了数学转化思想方法,考查了函数构造法,该题(3)巧妙地转化构造函数,使该题解题过程变得较为简洁,起到了事半功倍的效果,该题是难题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目