题目内容
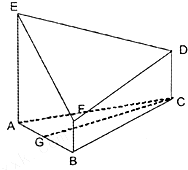 已知△ABC是正三角形,GC是△ABC的中线,EA、FB、CD都垂直于平面ABC.EA=3a,AB=CD=2a,FB=a,设平面EDF与平面ABC的交线为l.
已知△ABC是正三角形,GC是△ABC的中线,EA、FB、CD都垂直于平面ABC.EA=3a,AB=CD=2a,FB=a,设平面EDF与平面ABC的交线为l.(1)证明GC∥l;
(2)证明平面EABF与平面EDF垂直;
(3)求多面体ABCDEF的体积.
分析:(1)取EF中点H,连DH,HG,易证四边形HGCD是平行四边形,由线面平行的性质定理可证GC∥l;
(2))△ABC是正三角形,G是AB的中点,可证得CG⊥AB,而CG⊥AB,于是可证CG⊥平面ABFE,从而可证平面EABF⊥平面EDF;
(3)利用割补法可求得多面体ABCDEF的体积.
(2))△ABC是正三角形,G是AB的中点,可证得CG⊥AB,而CG⊥AB,于是可证CG⊥平面ABFE,从而可证平面EABF⊥平面EDF;
(3)利用割补法可求得多面体ABCDEF的体积.
解答: 证明:(1)取EF中点H,连DH,HG…1′
证明:(1)取EF中点H,连DH,HG…1′
在梯形EABF中,HG是梯形中位线,故HG∥DC,HG
=
=2a=CD,
∴四边形HGCD是平行四边形,…3′
∴CG∥DH,
∴CG∥平面EFD,平面EDF∩平面ABC=l
∴CG∥l…5′
(2)△ABC是正三角形,G是AB的中点,
∴CG⊥AB,
∵AE⊥CG,
∴CG⊥平面ABFE,
∴DH⊥平面ABFE,
∴平面EABF⊥平面EDF;…9′
(3)∵三棱柱EMN-ABC的体积V1=SABC•|AE|=
•2a•2a•sin60°•3a=3
a3,
而四棱锥E-MFDN的体积V2=
•SMFDN•h(h为该四棱锥的高,其数值为底面等边△EMN的底边MN上的高),
∴V2=
•
•h
=
•
•
a
=
a3,
∴多面体ABCDEF的体积V=V1-V2=3
a3-
a3=2
a3.…12′
 证明:(1)取EF中点H,连DH,HG…1′
证明:(1)取EF中点H,连DH,HG…1′在梯形EABF中,HG是梯形中位线,故HG∥DC,HG
| |EA|+|BF| |
| 2 |
| 3a+a |
| 2 |
∴四边形HGCD是平行四边形,…3′
∴CG∥DH,
∴CG∥平面EFD,平面EDF∩平面ABC=l
∴CG∥l…5′
(2)△ABC是正三角形,G是AB的中点,
∴CG⊥AB,
∵AE⊥CG,
∴CG⊥平面ABFE,
∴DH⊥平面ABFE,
∴平面EABF⊥平面EDF;…9′
(3)∵三棱柱EMN-ABC的体积V1=SABC•|AE|=
| 1 |
| 2 |
| 3 |
而四棱锥E-MFDN的体积V2=
| 1 |
| 3 |
∴V2=
| 1 |
| 3 |
| (|MF|+|DN|) |
| 2 |
=
| 1 |
| 3 |
| (2a+a)2a |
| 2 |
| 3 |
=
| 3 |
∴多面体ABCDEF的体积V=V1-V2=3
| 3 |
| 3 |
| 3 |
点评:本题考查直线与平面平行的性质,考查平面与平面垂直的判定及合几何体的体积问题,考查割补法,属于中档题.

练习册系列答案
相关题目

