题目内容
设向量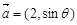 ,
,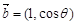 ,
,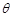 为锐角.
为锐角.
(1)若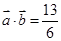 ,求
,求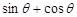 的值;
的值;
(2)若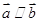 ,求
,求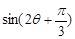 的值.
的值.
【答案】
(1)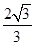 ;(2)
;(2)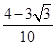 .
.
【解析】
试题分析:(1)利用向量数量积的坐标表示,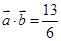 可转化为三角等式,然后利用三角函数的相关公式对其变形,求解则可得到
可转化为三角等式,然后利用三角函数的相关公式对其变形,求解则可得到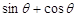 的值,求解过程中要注意由角的取值范围对结果进行适当取舍;(2)利用向量平行的坐标表示,可将
的值,求解过程中要注意由角的取值范围对结果进行适当取舍;(2)利用向量平行的坐标表示,可将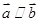 可转化为三角等式,通过对条件和问题的差异分析,利用三角函数的相关公式对其变形,可求出
可转化为三角等式,通过对条件和问题的差异分析,利用三角函数的相关公式对其变形,可求出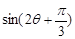 的值.
的值.
试题解析:(1)因为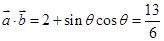 ,
所以
,
所以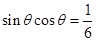 , 2分
, 2分
所以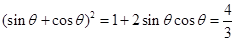 .
.
又因为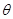 为锐角,所以
为锐角,所以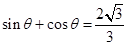 .
6分
.
6分
(2)因为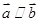 ,所以
,所以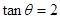 ,
8分
,
8分
所以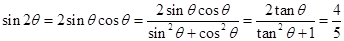 ,
10分
,
10分
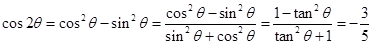 .
12分
.
12分
所以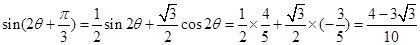 . 14分
. 14分
考点:两角和与差的三角函数、倍角公式、同角三角函数关系式.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,
, 且
且 ∥
∥ ,则锐角
,则锐角 为
。
为
。