题目内容
已知正长体ABCD—A1B1C1D1棱长为2,E、F、G分别为棱AA1、AB、BC的中点,在棱C1D1上求一点H,使E、F、G、H共面.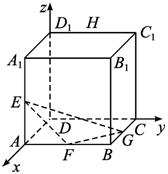
解析:建立如图所示的坐标,设H(0,y,z).
则![]() =(2,0,1)-(0,y,2)=(2,-y,-1),
=(2,0,1)-(0,y,2)=(2,-y,-1),
![]() =(2,1,0)-(0,y,2)=(2,1-y,-2),
=(2,1,0)-(0,y,2)=(2,1-y,-2),
![]() =(1,2,0)-(0,y,2)=(1,2-y,-2),
=(1,2,0)-(0,y,2)=(1,2-y,-2),
∵E、F、G、H共面,
∴![]() =m
=m![]() +n
+n![]() ,
,
即(2,1-y,-2)=(2m+n,-my+2n-ny,-m-2n).
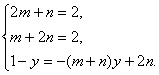 解得m=n=
解得m=n=![]() ,y=1.
,y=1.
故H(0,1,2)即为C1D1的中点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目