题目内容
已知点（m，n）在曲线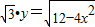
上，则m2+（n-1）2的取值范围是（ ）A．[1，2]
B．[1，3]
C．[1，4]
D．[1，9]
【答案】分析：可将
两端平方，化为椭圆方程（上半部分），将（m，n）代入方程，整理只含有n的关系式，利用n的取值范围即可求得m2+（n-1）2的取值范围．
解答：解：由
两端平方后整理得：
，
又点（m，n）在曲线
上，
∴
，∴
，
∴m2+（n-1）2=
=
（0≤n≤2），
∴
，即1≤m2+（n-1）2≤4．
故选C．
点评：本题考查椭圆的简单性质，着重考查学生的化归思想及综合应用知识解决问题的能力，属于中档题．
两端平方，化为椭圆方程（上半部分），将（m，n）代入方程，整理只含有n的关系式，利用n的取值范围即可求得m2+（n-1）2的取值范围．解答：解：由
两端平方后整理得：，又点（m，n）在曲线
上，∴
，∴，∴m2+（n-1）2=
=（0≤n≤2），∴
，即1≤m2+（n-1）2≤4．故选C．
点评：本题考查椭圆的简单性质，着重考查学生的化归思想及综合应用知识解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图，直线l1和l2相交于点M且l1⊥l2，点N∈l1．以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等．若△AMN为锐角三角形，
)为圆心，1为半径的圆相切，又知C的一个焦点与A关于y = x对称．
如图，直线l1和l2相交于点M且l1⊥l2，点N∈l1．以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等．若△AMN为锐角三角形，
，|AN|=3，且|BN|=6．