题目内容
O是锐角三角形ABC的外心,由O向边BC,CA,AB引垂线,垂足分别是D,E,F,给出下列命题:
①
+
+
=0;
②
+
+
=0;
③|
|:|
|:|
|=cosA:cosB:cosC;
④?λ∈R,使得
=λ(
+
).
以上命题正确的个数是( )
①
| OA |
| OB |
| OC |
②
| OD |
| OE |
| OF |
③|
| OD |
| OE |
| OF |
④?λ∈R,使得
| AD |
| ||
|
|
| ||
|
|
以上命题正确的个数是( )
分析:由O点是锐角三角形ABC的外心,利用外心的概念,结合向量加法的平行四边形法则得到向量
,
,
与向量
,
,
的关系,运用反证法的思想得到命题①②均不正确;
利用三角形外接圆半径的关系,把|
|:|
|:|
|转化为
:
:
,进一步转化为cos∠COD:cos∠AOE:cos∠BOF,借助于同弧所对圆心角是圆周角的2倍得到③|
|:|
|:|
|=cosA:cosB:cosC;
利用正弦定理把命题④中的sinB和sinC替换为三角形的边长和外接圆的半径,由
=
(
+
)替换整理可求出存在的实数λ的值.
| OD |
| OE |
| OF |
| OA |
| OB |
| OC |
利用三角形外接圆半径的关系,把|
| OD |
| OE |
| OF |
| OD |
| OC |
| OE |
| OA |
| OF |
| OB |
| OD |
| OE |
| OF |
利用正弦定理把命题④中的sinB和sinC替换为三角形的边长和外接圆的半径,由
| AD |
| 1 |
| 2 |
| AB |
| AC |
解答:解:因为O是锐角三角形ABC的外心,所以O在△ABC内部,由O向边BC,CA,AB引垂线,垂足分别是D,E,F,
则D,E,F分别为边BC,CA,AB的中点,
由向量加法的平行四边形法则可知,
+
=2
,
若
+
+
=
,则
=-(
+
),所以
=-2
,说明A,O,D一定共线,因为OD⊥BC,
所以AD⊥BC,则有AB=AC,而原三角形只是锐角三角形,不一定有AB=AC,所以命题①错误;
由
=
(
+
),
=
(
+
),
=
(
+
),
所以
+
+
=
(2
+2
+2
)=
+
+
,
因为命题①不正确,所以命题②不正确;
因为O是△ABC的外心,所以OA=OB=OC,又OD⊥BC,OE⊥AC,OF⊥AB
所以OD:OE:OF=
:
:
=cos∠COD:cos∠AOE:cos∠BOF,
∵∠COD=
∠BOC=∠A,∠AOE=
∠COA=∠B,∠BOF=
∠AOB=∠C,
∴OD:OE:OF=cosA:cosB:cosC,所以命题③正确;
在△ABC中,因为
=
=2R,
所以
+
=
(
+
),
因为
=
(
+
),若?λ∈R,使得
=λ(
+
),
即
=
(
+
),则
=
,所以λ=
.
所以?λ∈R,使得
=λ(
+
),所以命题④正确.
综上,正确命题是③④.
故选B.
则D,E,F分别为边BC,CA,AB的中点,
由向量加法的平行四边形法则可知,
| OB |
| OC |
| OD |
若
| OA |
| OB |
| OC |
| 0 |
| OA |
| OB |
| OC |
| OA |
| OD |
所以AD⊥BC,则有AB=AC,而原三角形只是锐角三角形,不一定有AB=AC,所以命题①错误;
由
| OD |
| 1 |
| 2 |
| OB |
| OC |
| OE |
| 1 |
| 2 |
| OC |
| OA |
| OF |
| 1 |
| 2 |
| OA |
| OB |
所以
| OD |
| OE |
| OF |
| 1 |
| 2 |
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
因为命题①不正确,所以命题②不正确;
因为O是△ABC的外心,所以OA=OB=OC,又OD⊥BC,OE⊥AC,OF⊥AB
所以OD:OE:OF=
| OD |
| OC |
| OE |
| OA |
| OF |
| OB |
∵∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴OD:OE:OF=cosA:cosB:cosC,所以命题③正确;
在△ABC中,因为
|
| ||
| sinB |
|
| ||
| sinC |
所以
| ||
|
|
| ||
|
|
| 2R | ||||
|
|
| AB |
| AC |
因为
| AD |
| 1 |
| 2 |
| AB |
| AC |
| AD |
| ||
|
|
| ||
|
|
即
| AD |
| 2λR | ||||
|
|
| AB |
| AC |
| 2λR | ||||
|
|
| 1 |
| 2 |
|
| ||||
| 4R |
所以?λ∈R,使得
| AD |
| ||
|
|
| ||
|
|
综上,正确命题是③④.
故选B.
点评:本题考查了命题的真假判断与应用,考查了三角形的外心,明确三角形的外心是三边中垂线的交点是关键,考查了平面向量在三角形中的应用,属中档题.

练习册系列答案
相关题目
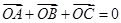 ;
;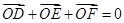 ;
;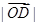 :
: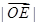 :
: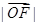 =cosA:cosB:cosC;
=cosA:cosB:cosC;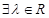 ,使得
,使得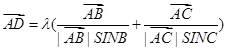 。
。