题目内容
已知函数 .
.
(Ⅰ)若a=-1,求函数f(x)的单调区间;
(Ⅱ)若?x>0,使f(x)≤0成立,求a的取值范围.
解:(Ⅰ)当a=-1时,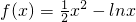
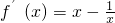 ,
,
令 ,解得x>1,所以f(x)的单调增区间为(1,+∞);
,解得x>1,所以f(x)的单调增区间为(1,+∞); ,解得0<x<1,所以f(x)的单调减区间为(0,1)
,解得0<x<1,所以f(x)的单调减区间为(0,1)
(Ⅱ)当a>0,由对数函数性质,f(x)的值域为R;
当a=0, >0,所以对?x>0,f(x)>0恒成立;
>0,所以对?x>0,f(x)>0恒成立;
当a<0,由 .令f′(x)=0,∴
.令f′(x)=0,∴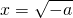
列表:
| x |  |  |  |
| f′(x) | _ | 0 | + |
| f(x) | 减函数 | 极小值 | 增函数 |
这是 .
.
∵?x>0,使f(x)≤0成立,∴ ,∴a≤-e,
,∴a≤-e,
∴a范围为(-∞,-e]∪(0,+∞).
分析:(Ⅰ)先求出其导函数,让其大于0求出增区间,小于0求出减区间即可;
(Ⅱ)先由a>0得f(x)的值域为R;a=0,
 >0满足要求;再对a<0时,求出其导函数,利用导函数研究出其极小值,与0相比即可求得结论.
>0满足要求;再对a<0时,求出其导函数,利用导函数研究出其极小值,与0相比即可求得结论.点评:本题第二问考查利用导函数来研究函数的极值.在利用导函数来研究函数的极值时,分三步①求导函数,②求导函数为0的根,③判断根左右两侧的符号,若左正右负,原函数取极大值;若左负右正,原函数取极小值.

练习册系列答案
相关题目
 .
.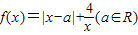 .
.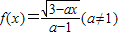 .
.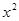 -ax-3(
-ax-3(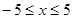 )
)