题目内容

△ABC的内角A、B、C的对边分别为a、b、c，若b²=ac，且sinC=2sinA，则cosB等于

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

B
分析：由正弦定理与sinC=2sinA，可解得c=2a，将这些代入由余弦定理得出的关于cosB的方程即可求出．
解答：∵sinC=2sinA，
∴由正弦定理得c=2a，
由余弦定理得b²=a²+c²-2accosB，
将b²=ac及c=2a代入上式解得
$\text{[math]}$ ．
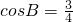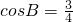故选B．
点评：考查正弦定理与余弦定理，属于运用定理建立所求量的方程通过解方程来求值的题目；训练目标是灵活运用公式求值．

练习册系列答案

中考信息猜想卷系列答案

中考专辑精通中考系列答案

中考锦囊系列答案

中考状元系列答案

中考总复习系列答案

掌控中考系列答案

68所名校图书毕业升学全真模拟试卷系列答案

国华图书中考拐点系列答案

创新能力学习中考总复习系列答案

核按钮系列答案

相关题目

设△ABC的内角A、B、C所对的边分别为a、b、c，已知a=1，b=2，cosC=

（Ⅰ）求△ABC的周长；
（Ⅱ）求cos（A-C）的值．

（2013•唐山二模）△ABC的内角A，B，C的对边分别为a，b，c，△ABC的面积S=

(c2-a2-b2)．
（Ⅰ）求C；
（Ⅱ）若a+b=2，且c=

（2011•宝坻区一模）设函数f（x）=sinx+cos（x+

），x∈R
（Ⅰ）求函数f（x）的最小正周期和值域；
（Ⅱ）记△ABC的内角A，B，C的对边分别为a，b，c，若f（A）=

b，求角C的值．

△ABC的内角A、B、C的对边分别为a、b、c，三边长a、b、c成等比数列，且a²=c²+ac-bc，则

（2013•上海）已知△ABC的内角A、B、C所对的边分别是a、b、c，若3a²+2ab+3b²-3c²=0，则角C的大小是