Question

（2013•石景山区二模）已知正六边形ABCDEF的边长是2，一条抛物线恰好经过该六边形的四个顶点，则抛物线的焦点到准线的距离是（　　）

• A．

  3

  4

• B．

  3

  2

• C．

  3

• D．2

  3

Answer 1

分析：如图，设正六边形ABCDEF的顶点A、B、C、F在抛物线y²=2px上．根据抛物线的对称性，设A（x₁，1），F（x₂，2），由抛物线方程和正六边形的性质建立关于x₁、x₂和p的方程组，解之可得2p=

3

，由此即可得到抛物线焦点到准线的距离．

解答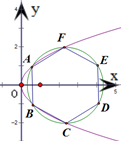：解：由题意，设正六边形ABCDEF的顶点A、B、C、F在抛物线y²=2px上，
设A（x₁，1），F（x₂，2），可得

x1+ 3 =x2      ① 2px1=1            ②  2px2=4            ③

，
由②、③消去p得x₂=4x₁，代入①可得x 1+

3

=4x1，
所以x₁=

3

3

，代入②得2p=

3

，
根据抛物线的性质，可得焦点到准线的距离是p=

3

2

故选：B

点评：本题给出边长为2正六边形ABCDEF，抛物线恰好经过六边形的四个顶点，求抛物线的焦准距．着重考查了抛物线的标准方程、简单几何性质和正六边形的性质等知识，属于中档题．