题目内容
18.已知函数f(x)=|2x-m|+m.(Ⅰ)若不等式f(x)≤6的解集为{x|-1≤x≤3},求实数m的值;
(Ⅱ)在(Ⅰ)的条件下,求使f(x)≤a-f(-x)有解的实数a的取值范围.
分析 (Ⅰ)求得不等式f(x)≤6的解集为m-3≤x≤3,再根据不等式f(x)≤6的解集为{x|-1≤x≤3},可得m-3=-1,由此求得m的范围.
(Ⅱ)令g(x)=f(x)+f(-x)=|2x-2|+|2x+2|+4的最小值,可得a的范围.
解答 解:(Ⅰ)∵函数f(x)=|2x-m|+m,不等式f(x)≤6的解集为{x|-1≤x≤3},
∴|2x-m|≤6-m 的解集为{x|-1≤x≤3}.
由|2x-m|≤6-m,可得m-6≤2x-m≤6-m,求得m-3≤x≤3,故有m-3=-1,m=2.
(Ⅱ)在(Ⅰ)的条件下,f(x)=|2x-m|+2,令g(x)=f(x)+f(-x)=|2x-2|+|2x+2|+4=$\left\{\begin{array}{l}{4-4x,x≤-1}\\{8,-1<x≤1}\\{4+4x,x>1}\end{array}\right.$,
故g(x)的最小值为8,
故使f(x)≤a-f(-x)有解的实数a的范围为[8,+∞).
点评 本题主要考查绝对值不等式的解法,分段函数的应用,求函数的最小值,函数的能成立问题,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
8.已知0<α<$\frac{π}{2}$,则sinα,α,tanα的大小关系为( )
| A. | tanα>sinα>α | B. | α>tanα>sinα | C. | sinα>α>tanα | D. | tanα>α>sinα |
9.设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与抛物线y2=8x有一个公共的焦点F,两曲线的一个交点为M.若|MF|=5,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
6.m,n,l是直线,α,β是两个不同的平面,下面说法正确的是( )
| A. | 若m∥α,m∥β,则α∥β | |
| B. | 若m⊥α,m?β,则α⊥β | |
| C. | 若m?α,n?α,m,n是异面直线,则n与α相交 | |
| D. | 若m?α,n?α,l⊥m,l⊥n,则l⊥α |
13.设直线l,m,平面α,β,下列条件能得出α∥β的是( )
| A. | l?α,m?α且l∥β,m∥β | B. | l?α,m?β且l∥m | ||
| C. | l⊥α,m⊥β且l∥m | D. | l∥α,m∥β且l∥m |
10.下列图象表示的函数中,不能用二分法求零点的是( )
| A. |  | B. | 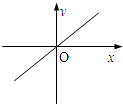 | C. |  | D. | 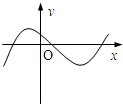 |
8.函数$y=\frac{1}{2}cos2x$的周期为( )
| A. | π | B. | 2π | C. | 4π | D. | $\frac{π}{4}$ |