题目内容
在△ABC中,cosA=
,tan(B-A)=
,则tanC=
.
| 3 |
| 5 |
| 1 |
| 2 |
| 41 |
| 38 |
| 41 |
| 38 |
分析:由同角三角函数的关系,算出sinA=
,可得tanA=
=
.根据tan(B-A)=
,利用两角差的正切公式,算出tanB=
,从而得出tan(B+A)=
.最后根据正切的诱导公式和三角形内角和定理,即可算出tanC的值.
| 4 |
| 5 |
| sinA |
| cosA |
| 4 |
| 3 |
| 1 |
| 2 |
| 11 |
| 2 |
| 11 |
| 2 |
解答:解:∵在△ABC中,cosA=
>0,
∴A为锐角,sinA=
=
.
即tanA=
=
.
∵tan(B-A)=
=
,
∴
=
,解得tanB=
.
∵tan(B+A)=
=-
,
∴tanC=tan(π-A-B)=-tan(B+A)=
.
故答案为:
.
| 3 |
| 5 |
∴A为锐角,sinA=
| 1-cos2A |
| 4 |
| 5 |
即tanA=
| sinA |
| cosA |
| 4 |
| 3 |
∵tan(B-A)=
| tanB-tanA |
| 1+tanBtanA |
| 1 |
| 2 |
∴
tanB-
| ||
1+tanB×
|
| 1 |
| 2 |
| 11 |
| 2 |
∵tan(B+A)=
| tanB+tanA |
| 1-tanBtanA |
| 41 |
| 38 |
∴tanC=tan(π-A-B)=-tan(B+A)=
| 41 |
| 38 |
故答案为:
| 41 |
| 38 |
点评:本题着重考查了三角形内角和定理、两角和与差的正切公式、同角三角函数的关系和诱导公式等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
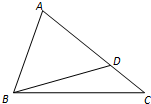 如图,在△ABC中,cos∠ABC=
如图,在△ABC中,cos∠ABC=