题目内容
 (12分)如图所示的几何体中,四边形ABCD是正方形,MA
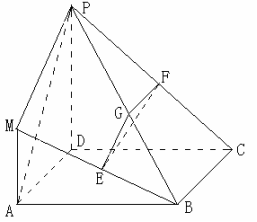
(12分)如图所示的几何体中,四边形ABCD是正方形,MA![]() 平面ABCD,PD∥MA,E、F、G分别为MB、PC、PB的中点,且AD=PD=2MA.
平面ABCD,PD∥MA,E、F、G分别为MB、PC、PB的中点,且AD=PD=2MA.
(1)求证:平面EFG∥平面ADMP;
(2)求三棱锥P-MAB与四棱锥P-ABCD的体积之比.
(1)证明:∵F、G为PC、PB中点 ∴FG∥BC又BC∥AD
∴FG∥AD ∵E、G为BM、PB中点 ∴EG∥PM又EG∩FG=G
∴平面EFG∥平面ADMP …………………………6分
(2)不妨设AB=2![]()
则![]()
![]() 所以
所以![]() …………………………12分
…………………………12分
附加题(本大题共2小题,每题10分,共20分)

练习册系列答案
相关题目
 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD为平行四边形,∠ACB=90°,EF∥BC,AC=BC=
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD为平行四边形,∠ACB=90°,EF∥BC,AC=BC= (2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1,
(2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1, (2010•吉安二模)如图所示的几何体中,底面ABCD是矩形,AB=9,BC=6,EF∥平面ABCD,EF=3,△ADE和△BCF
(2010•吉安二模)如图所示的几何体中,底面ABCD是矩形,AB=9,BC=6,EF∥平面ABCD,EF=3,△ADE和△BCF (2013•西城区一模)在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,
(2013•西城区一模)在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD, 在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.