题目内容
偶函数g(x)在[0,+∞)是减函数,若不等式g(mx-1)>g(2+x2)恒成立,则实数m的范围是( )
分析:根据已知结合偶函数在对称区间上单调性相反,可分析出函数的单调性,进而将不等式g(mx-1)>g(2+x2)转化为|mx-1|<|2+x2|,再由二次函数的图象和性质,构造关于m的不等式组,解出m的范围.
解答:解:∵偶函数g(x)在[0,+∞)上是减函数,
∴函数g(x)在(-∞,0]上是增函数,
若不等式g(mx-1)>g(2+x2)恒成立,
则表示|mx-1|<|2+x2|=2+x2恒成立,
即-(2+x2)<mx-1<2+x2恒成立
即
恒成立
故
解得m∈(-2,2)
故选B
∴函数g(x)在(-∞,0]上是增函数,
若不等式g(mx-1)>g(2+x2)恒成立,
则表示|mx-1|<|2+x2|=2+x2恒成立,
即-(2+x2)<mx-1<2+x2恒成立
即
|
故
|
解得m∈(-2,2)
故选B
点评:本题考查的知识点是函数的奇偶性,函数的单调性,不等式恒成立,是函数图象与性质的综合考查,难度稍大,属于中档题

练习册系列答案
相关题目
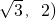
 ,2
,2