题目内容
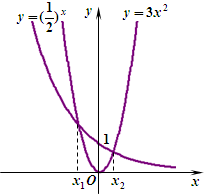
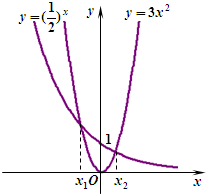 如图,是函数y=(
如图,是函数y=(| 1 |
| 2 |
给出如下两个命题:
①当x<x1时,(
| 1 |
| 2 |
②当x>x2时,(
| 1 |
| 2 |
(1)举出一个反例,说明命题①是假命题;
(2)利用基本函数的单调性,说明命题②是真命题.
分析:(1)利用条件,举出反例即可.(2)利用函数的单调性的定义证明命题.
解答:解:(1)可以举反例:取x=-10,则x<x1,
但(
)-10=1024,3×(-10)2=300,∴(
)x<3x2不成立;
(2)∵函数y=(
)x在[x2,+∞)上是减函数,函数y=3x2在[x2,+∞)上是增函数,
∴当x>x2时,(
)x<(
)x2=3
<3x2.
但(
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵函数y=(
| 1 |
| 2 |
∴当x>x2时,(
| 1 |
| 2 |
| 1 |
| 2 |
| x | 2 2 |
点评:本题主要考查指数函数和二次函数的图象和性质.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 如图,是函数y=f(x)的导函数f′(x)的图象,则下面判断正确的是( )
如图,是函数y=f(x)的导函数f′(x)的图象,则下面判断正确的是( )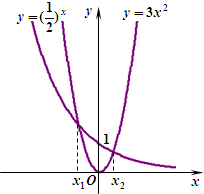 如图,是函数
如图,是函数