Question

（本题满分12分）已知函数,当x = -1时取得极大值7，当x = 3时

取得极小值；

(1)求的值；  

（2）求的极小值。

 

Answer 1

【答案】

∵f (x) = x³ + ax² +bx + c ,∴f′ (x) = 3x² +2ax +b （2分）

      ∵当x = - 1 时函数取得极大值7，当x = 3时取得极小值

      ∴x = - 1 和x = 3是方程f′ (x)=0的两根，有

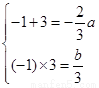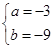     ∴，  ∴f (x) = x³ – 3x² – 9x + c（6分）

∵当x = -1时，函数取极大值7，∴( - 1 )³ – 3( - 1 )² – 9( - 1) + c = 7,∴c = 2（9分）

此时函数f (x)的极小值为：f（3）= 3³ - 3×3² - 9×3×2 = - 25（12分）

 

【解析】略