题目内容
 如图,已知函数f(x)=Asin(ωx+φ)(A>0,|φ|<
如图,已知函数f(x)=Asin(ωx+φ)(A>0,|φ|< )图象上一个最高点坐标为(2,2
)图象上一个最高点坐标为(2,2 ),这个最高点到相邻最低点的图象与x轴交于点(5,0).
),这个最高点到相邻最低点的图象与x轴交于点(5,0).
(1)求f(x)的解析式;
(2)是否存在正整数m,使得将函数f(x)的图象向右平移m个单位后得到一个偶函数的图象?若存在,求m的最小值;若不存在,请说明理由.
解:(1)由图象知A=2 ,
, =3,
=3,
∴T=12,∴ω=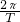 =
= ,
,
∴f(x)=2 sin(
sin( x+φ),
x+φ),
∵图象过(2,2 ),∴2
),∴2 =2
=2 sin(
sin( ×2+φ),
×2+φ),
∴sin( ×2+φ)=1,
×2+φ)=1,
令 +φ=
+φ= ,∴φ=
,∴φ= ,
,
∴f(x)=2 sin(
sin( x+
x+ ).
).
(2)假设存在m,则有
f(x-m)=2 sin[
sin[ (x-m)+
(x-m)+ ]=2
]=2 sin[
sin[ x+
x+ (1-m)]
(1-m)]
∵f(x-m)为偶函数,
∴ (1-m)=
(1-m)= ,k∈Z
,k∈Z
∴m=-6k-2,∴k=-1时m=4.
∴存在m,m的最小值为4.
分析:(1)利用三角函数的图象确定A,ω,φ.其中最值确定A,周期大小确定ω,利用定点(2,2 ),确定φ.
),确定φ.
(2)利用函数的平移得到偶函数的条件,然后求出m.
点评:本题的考点是三角函数的图象和性质,以及三角函数的图象平移,要求熟练掌握三角函数之间的变换技巧.
 ,
, =3,
=3,∴T=12,∴ω=
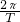 =
= ,
,∴f(x)=2
 sin(
sin( x+φ),
x+φ),∵图象过(2,2
 ),∴2
),∴2 =2
=2 sin(
sin( ×2+φ),
×2+φ),∴sin(
 ×2+φ)=1,
×2+φ)=1,令
 +φ=
+φ= ,∴φ=
,∴φ= ,
,∴f(x)=2
 sin(
sin( x+
x+ ).
).(2)假设存在m,则有
f(x-m)=2
 sin[
sin[ (x-m)+
(x-m)+ ]=2
]=2 sin[
sin[ x+
x+ (1-m)]
(1-m)]∵f(x-m)为偶函数,
∴
 (1-m)=
(1-m)= ,k∈Z
,k∈Z∴m=-6k-2,∴k=-1时m=4.
∴存在m,m的最小值为4.
分析:(1)利用三角函数的图象确定A,ω,φ.其中最值确定A,周期大小确定ω,利用定点(2,2
 ),确定φ.
),确定φ.(2)利用函数的平移得到偶函数的条件,然后求出m.
点评:本题的考点是三角函数的图象和性质,以及三角函数的图象平移,要求熟练掌握三角函数之间的变换技巧.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 如图,已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则函数f(x)=
如图,已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,则函数f(x)= 6、如图是已知函数f(x)=x2-3x+5,求当x∈{0,3,6,…60}时的函数值的一个程序框图,则①处应填( )
6、如图是已知函数f(x)=x2-3x+5,求当x∈{0,3,6,…60}时的函数值的一个程序框图,则①处应填( ) 如图,已知函数f(x)=Asin(ωx+φ)(A>0,|φ|<
如图,已知函数f(x)=Asin(ωx+φ)(A>0,|φ|<
