题目内容
设函数
，若f（a）＞1，则实数a的取值范围是
- A.（-2，1）
- B.（-∞，-2）∪（2，+∞）
- C.（1，+∞）
- D.（-∞，-1）∪（0，+∞）
B
分析：当a＜0时，由 f（a）=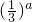
-8＞1求得a得范围．当a≥0时，由 f（a）=a2-a-1＞1，求得a得范围．再把这两个a的范围取并集，即得所求．
解答：当a＜0时，由 f（a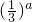）=-8＞1可得 3-a＞32，故-a＞2，解得 a＜-2．
当a≥0时，由 f（a）=a2-a-1＞1可得 （a-2）（a+1）＞0，解得 a＜-1（舍去），或 a＞2．
综上可得，实数a的取值范围为 （-∞，-2）∪（2，+∞），
故选B．
点评：本题主要考查分段函数的应用，解指数不等式和一元二次不等式，体现了分类讨论的数学思想，属于中档题．
分析：当a＜0时，由 f（a）=
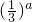-8＞1求得a得范围．当a≥0时，由 f（a）=a2-a-1＞1，求得a得范围．再把这两个a的范围取并集，即得所求．解答：当a＜0时，由 f（a）=
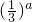-8＞1可得 3-a＞32，故-a＞2，解得 a＜-2．当a≥0时，由 f（a）=a2-a-1＞1可得 （a-2）（a+1）＞0，解得 a＜-1（舍去），或 a＞2．
综上可得，实数a的取值范围为 （-∞，-2）∪（2，+∞），
故选B．
点评：本题主要考查分段函数的应用，解指数不等式和一元二次不等式，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
，若f（a）＞1，则a的取值范围是（ ）
，若f（a）+f（-1）=2，则a=（ ）
，若f（a）＞1，则实数a的取值范围是（ ）
，若f（a）=2，则实数a= ．
，若f（a）＞1，则实数a的取值范围是（ ）