题目内容
已知函数f(x)=
.(Ⅰ)设a=(2，-1)，b=(cosx，sinx)，若a·b=0，求此时f(x)的值；
(Ⅱ)设g(x)=f(x-
)+sin(2x-
)，x∈[
)，求g(x)的最大值．
解：(Ⅰ)f(x)=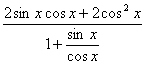
=
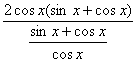
=2cos2x(tanx≠-1)
由a·b=0，有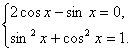 ∴cos2x=
故此时f(x)=
.
(Ⅱ)g(x)=2cos2(x-
)+sin(2x-
)
=1+cos(2x-
)+sin(2x-
)
=1+
sin(2x-
+
)=1+
sin2x．
由x∈[
)，有
≤2x≤π．
∴当x=
时，g(x)的最大值为1+
．
练习册系列答案
相关题目
已知函数f(x)=
|
A、(
| ||||
B、（
| ||||
C、（
| ||||
D、[
|