题目内容
设函数f(x)=ln(x+a)+x2
(I)若当x=-1时,f(x)取得极值,求a的值,并讨论f(x)的单调性;
(II)若f(x)存在极值,求a的取值范围,并证明所有极值之和大于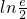 .
.
解:(Ⅰ)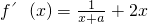 ,
,
依题意有f'(-1)=0,故 .
.
从而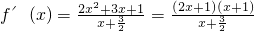 .
.
f(x)的定义域为 ,当
,当 时,f'(x)>0;
时,f'(x)>0;
当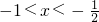 时,f'(x)<0;
时,f'(x)<0;
当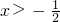 时,f'(x)>0.
时,f'(x)>0.
从而,f(x)分别在区间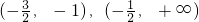 单调增加,在区间
单调增加,在区间 单调减少.
单调减少.
(Ⅱ)f(x)的定义域为(-a,+∞),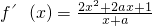 .
.
方程2x2+2ax+1=0的判别式△=4a2-8.
(ⅰ)若△<0,即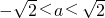 ,在f(x)的定义域内f'(x)>0,故f(x)的极值.
,在f(x)的定义域内f'(x)>0,故f(x)的极值.
(ⅱ)若△=0,则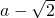 或
或 .
.
若 ,
,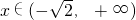 ,
,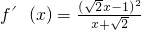 .
.
当 时,f'(x)=0,
时,f'(x)=0,
当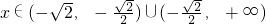 时,f'(x)>0,所以f(x)无极值.
时,f'(x)>0,所以f(x)无极值.
若 ,
, ,
,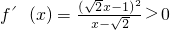 ,f(x)也无极值.
,f(x)也无极值.
(ⅲ)若△>0,即 或
或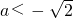 ,则2x2+2ax+1=0有两个不同的实根
,则2x2+2ax+1=0有两个不同的实根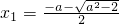 ,
,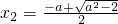 .
.
当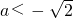 时,x1<-a,x2<-a,从而f'(x)有f(x)的定义域内没有零点,
时,x1<-a,x2<-a,从而f'(x)有f(x)的定义域内没有零点,
故f(x)无极值.
当 时,x1>-a,x2>-a,f'(x)在f(x)的定义域内有两个不同的零点,
时,x1>-a,x2>-a,f'(x)在f(x)的定义域内有两个不同的零点,
由根值判别方法知f(x)在x=x1,x=x2取得极值.
综上,f(x)存在极值时,a的取值范围为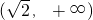 .
.
f(x)的极值之和为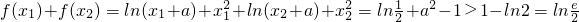 .
.
分析:(I)先求函数定义域,然后对函数求导,由题意可得,f′(-1)=0,代入可求a,代入a的值,分别解f′(x)>0,f′(x)<0,求解即可.
(II)由题意可得在区间(-a,+∞)上,f′(x)=0有根,结合一元二次方程根的存在情况讨论该方程的△=4a2-8,求a的取值范围,结合a的取值,把极值点代入函数f(x)可得,
点评:本题考查利用导数研究函数的极值及单调性,解题时若含有参数,要对参数的取值进行讨论,而分类讨论的思想也是高考的一个重要思想,要注意体会其在解题中的运用.
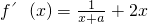 ,
,依题意有f'(-1)=0,故
 .
.从而
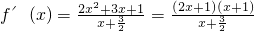 .
.f(x)的定义域为
 ,当
,当 时,f'(x)>0;
时,f'(x)>0;当
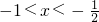 时,f'(x)<0;
时,f'(x)<0;当
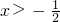 时,f'(x)>0.
时,f'(x)>0.从而,f(x)分别在区间
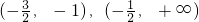 单调增加,在区间
单调增加,在区间 单调减少.
单调减少.(Ⅱ)f(x)的定义域为(-a,+∞),
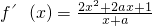 .
.方程2x2+2ax+1=0的判别式△=4a2-8.
(ⅰ)若△<0,即
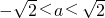 ,在f(x)的定义域内f'(x)>0,故f(x)的极值.
,在f(x)的定义域内f'(x)>0,故f(x)的极值.(ⅱ)若△=0,则
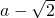 或
或 .
.若
 ,
,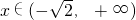 ,
,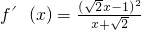 .
.当
 时,f'(x)=0,
时,f'(x)=0,当
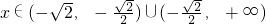 时,f'(x)>0,所以f(x)无极值.
时,f'(x)>0,所以f(x)无极值.若
 ,
, ,
,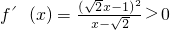 ,f(x)也无极值.
,f(x)也无极值.(ⅲ)若△>0,即
 或
或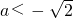 ,则2x2+2ax+1=0有两个不同的实根
,则2x2+2ax+1=0有两个不同的实根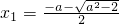 ,
,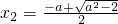 .
.当
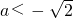 时,x1<-a,x2<-a,从而f'(x)有f(x)的定义域内没有零点,
时,x1<-a,x2<-a,从而f'(x)有f(x)的定义域内没有零点,故f(x)无极值.
当
 时,x1>-a,x2>-a,f'(x)在f(x)的定义域内有两个不同的零点,
时,x1>-a,x2>-a,f'(x)在f(x)的定义域内有两个不同的零点,由根值判别方法知f(x)在x=x1,x=x2取得极值.
综上,f(x)存在极值时,a的取值范围为
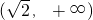 .
.f(x)的极值之和为
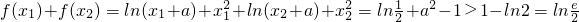 .
.分析:(I)先求函数定义域,然后对函数求导,由题意可得,f′(-1)=0,代入可求a,代入a的值,分别解f′(x)>0,f′(x)<0,求解即可.
(II)由题意可得在区间(-a,+∞)上,f′(x)=0有根,结合一元二次方程根的存在情况讨论该方程的△=4a2-8,求a的取值范围,结合a的取值,把极值点代入函数f(x)可得,

点评:本题考查利用导数研究函数的极值及单调性,解题时若含有参数,要对参数的取值进行讨论,而分类讨论的思想也是高考的一个重要思想,要注意体会其在解题中的运用.

练习册系列答案
相关题目