题目内容
11.对于椭圆x2-my2=1(|m|<1),给出下列命题:①焦点在x轴上;
②长半轴的长是$\frac{1}{\sqrt{m}}$;
③短半轴的长是1;
④焦点到中心的距离$\sqrt{-\frac{1+m}{m}}$;
⑤离心率e=$\sqrt{1+m}$.
其中正确命题的序号是③④⑤.
分析 对于椭圆x2-my2=1(|m|<1),化为${x}^{2}+\frac{{y}^{2}}{\frac{1}{-m}}$=1,因此-1<m<0,$\frac{1}{-m}$>1.于是:a=$\sqrt{\frac{1}{-m}}$,b=1,c=$\sqrt{-\frac{1+m}{m}}$,即可得出.
解答 解:对于椭圆x2-my2=1(|m|<1),化为${x}^{2}+\frac{{y}^{2}}{\frac{1}{-m}}$=1,因此-1<m<0,$\frac{1}{-m}$>1.
∴椭圆的焦点在y轴上,长半轴的长=$\sqrt{\frac{1}{-m}}$,短半轴的长是1,焦点到中心的距离c=$\sqrt{\frac{1}{-m}-1}$=$\sqrt{-\frac{1+m}{m}}$,离心率e=$\frac{\sqrt{-\frac{1+m}{m}}}{\sqrt{\frac{1}{-m}}}$=$\sqrt{1+m}$.
综上可得:正确的是③④⑤.
故答案为:③④⑤.
点评 本题考查了椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.下列对应是从集合S到T的映射的是( )
| A. | S={0,1,4,9},T={-3,-2,-1,0,1,2,3},对应法则是开平方 | |
| B. | S={0,1,2,5},T=$\{1,\frac{1}{2},\frac{1}{5}\}$,对应法则是取倒数 | |
| C. | S=N,T={-1,1},对应法则是n→(-1)n,n∈S | |
| D. | S={x|x∈R},T={y|y∈R},对应法则是x→y=$\frac{1+x}{1-x}$ |
6.一个几何体的三视图如图所示,则该几何体的体积是( )
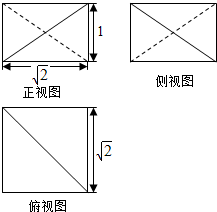

| A. | $\frac{5}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
 如图,在四边形ABCB′,△ABC≌△AB′C,AB⊥AB′,cos∠BCB′=$\frac{3}{4}$,BC=2$\sqrt{2}$.
如图,在四边形ABCB′,△ABC≌△AB′C,AB⊥AB′,cos∠BCB′=$\frac{3}{4}$,BC=2$\sqrt{2}$.