题目内容
已知等比数列{an}中,2a4-3a3+a2=0,且a1=64,公比q≠1,(1)求an;
(2)设bn=log2an,求数列{|bn|}的前n项和Tn.
【答案】分析:(1)由题设可知,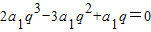 ,解出q,根据等比数列通项公式可得an;
,解出q,根据等比数列通项公式可得an;
(2)由(1)可得bn=7-n,易知n≤7时,bn≥0,n>7时bn<0,分n≤7,n>7两种情况进行讨论去掉绝对值符号,利用等差数列求和公式可得Tn.
解答:解:(1)由题设可知,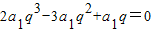 ,
,
又a1≠0,q≠0,故2q2-3q+1=0⇒(2q-1)(q-1)=0,解得q=1或 ,
,
又由题设q≠1,∴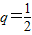 .
.
从而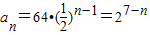 ;
;
(2)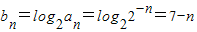 ,
,
当n≤7时,bn≥0,n>7时bn<0,
故n≤7时,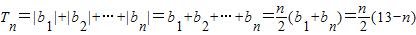 ;
;
n>7时,Tn=|b1|+|b2|+…+|bn|=b1+b2+…+b7-b8-b9…bn
=-(b1+b2+…+bn)+2(b1+b2+…+b7)
=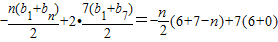 =
=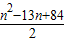 ,
,
综上可得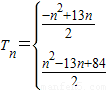
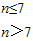 .
.
点评:本题考查等比数列的通项公式、等差数列的求和,考查学生的运算求解能力,属中档题.
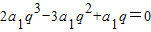 ,解出q,根据等比数列通项公式可得an;
,解出q,根据等比数列通项公式可得an;(2)由(1)可得bn=7-n,易知n≤7时,bn≥0,n>7时bn<0,分n≤7,n>7两种情况进行讨论去掉绝对值符号,利用等差数列求和公式可得Tn.
解答:解:(1)由题设可知,
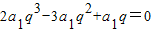 ,
,又a1≠0,q≠0,故2q2-3q+1=0⇒(2q-1)(q-1)=0,解得q=1或
 ,
,又由题设q≠1,∴
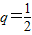 .
.从而
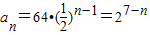 ;
;(2)
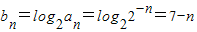 ,
,当n≤7时,bn≥0,n>7时bn<0,
故n≤7时,
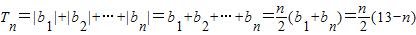 ;
;n>7时,Tn=|b1|+|b2|+…+|bn|=b1+b2+…+b7-b8-b9…bn
=-(b1+b2+…+bn)+2(b1+b2+…+b7)
=
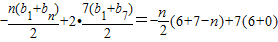 =
=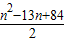 ,
,综上可得
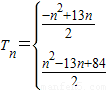
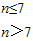 .
.点评:本题考查等比数列的通项公式、等差数列的求和,考查学生的运算求解能力,属中档题.

练习册系列答案
相关题目