题目内容
设数列{an}满足a1+3a2+32a3+…+3n-1an=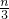 ,n∈N*.
,n∈N*.
(1)求数列{an}的通项;
(2)设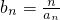 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
解:(1)∵a1+3a2+32a3+…+3n-1an=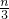 ,①
,①
∴当n≥2时,a1+3a2+32a3+…+3n-2an-1= .②
.②
①-②,得3n-1an= ,
, (n≥2),
(n≥2),
在①中,令n=1,
得 .∴
.∴ .
.
(2)∵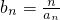 ,
,
∴bn=n•3n.
∴Sn=3+2×32+3×33+…+n•3n.③
∴3Sn=32+2×33+3×34+…+n•3n+1.④
④-③,得2Sn=n•3n+1-(3+32+33+…+3n),
即2Sn=n•3n+1-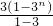 .
.
∴ .
.
分析:(1)由a1+3a2+32a3+…+3n-1an=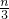 ?当n≥2时,a1+3a2+32a3+…+3n-2an-1=
?当n≥2时,a1+3a2+32a3+…+3n-2an-1= ,两式作差求出数列{an}的通项.
,两式作差求出数列{an}的通项.
(2)由(1)的结论可知数列{bn}的通项.再用错位相减法求和即可.
点评:本题的第二问考查了数列求和的错位相减法.错位相减法适用于通项为一等差数列乘一等比数列组成的新数列.
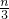 ,①
,①∴当n≥2时,a1+3a2+32a3+…+3n-2an-1=
 .②
.②①-②,得3n-1an=
 ,
, (n≥2),
(n≥2),在①中,令n=1,
得
 .∴
.∴ .
.(2)∵
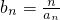 ,
,∴bn=n•3n.
∴Sn=3+2×32+3×33+…+n•3n.③
∴3Sn=32+2×33+3×34+…+n•3n+1.④
④-③,得2Sn=n•3n+1-(3+32+33+…+3n),
即2Sn=n•3n+1-
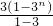 .
.∴
 .
.分析:(1)由a1+3a2+32a3+…+3n-1an=
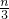 ?当n≥2时,a1+3a2+32a3+…+3n-2an-1=
?当n≥2时,a1+3a2+32a3+…+3n-2an-1= ,两式作差求出数列{an}的通项.
,两式作差求出数列{an}的通项.(2)由(1)的结论可知数列{bn}的通项.再用错位相减法求和即可.
点评:本题的第二问考查了数列求和的错位相减法.错位相减法适用于通项为一等差数列乘一等比数列组成的新数列.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
设数列{an}满足a1=1,a2+a4=6,且对任意n∈N*,函数f(x)=(an-an+1+an+2)x+an+1?cosx-an+2sinx满足f′(
)=0若cn=an+
,则数列{cn}的前n项和Sn为( )
| π |
| 2 |
| 1 |
| 2an |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|