Question

A={x|-2＜x≤5}，B={x|m+1≤x≤2m-1}，若B⊆A，则m的取值范围是

（-∞，3]

．

Answer 1

分析：讨论集合B=∅和B≠∅时，利用条件B⊆A，确定不等式关系，即可求m的取值范围．

解答：解：若B=∅，即m+1＞2m-1，解得m＜1，满足条件B⊆A，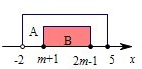
若B≠∅，即m+1≤2m-1，解得m≥1，要使B⊆A，
则满足

m+1＞-2 2m-1≤5

，即

m＞-3 m≤3

，解得-3＜m≤3，此时1≤m≤3．
综上：m≤3．
故答案为：（-∞，3]．

点评：本题主要考查集合关系的应用，利用数轴确定集合端点之间的关系是解决此类问题的基本方法，注意端点处等号的取舍．