题目内容
已知f（x）是二次函数，不等式f（x）＜0的解集是（0，5），且f（x）在区间[-1，4]上的最大值是12。（1）求f（x）的解析式；
（2）是否存在实数m，使得方程 f（x）+
=0在区间（m，m+1）内有且只有两个不等的实数根？若存在，求出m的取值范围；若不存在，说明理由。
（2）是否存在实数m，使得方程 f（x）+
=0在区间（m，m+1）内有且只有两个不等的实数根？若存在，求出m的取值范围；若不存在，说明理由。解：（1）∵f（x）是二次函数，且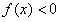
的解集是
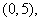
∴可设
∴f（x）在区间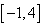
上的最大值是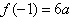
由已知，得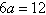
∴a=2
∴
。
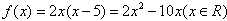（2）方程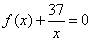
等价于方程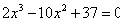
设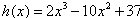
则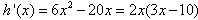
当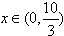
时，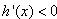
，h（x）是减函数
当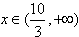
时，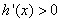
，h（x）是增函数
∵
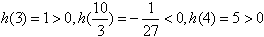
∴方程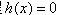
在区间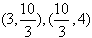
内分别有惟一实数根，
而在区间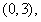
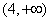内没有实数根
所以存在惟一的自然数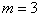
，使得方程
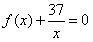在区间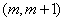
内有且只有两个不同的实数根。
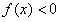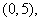
的解集是∴可设
∴f（x）在区间
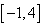上的最大值是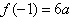由已知，得
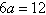
∴a=2
∴
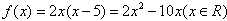。（2）方程
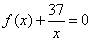等价于方程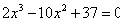设
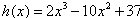
则
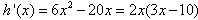
当
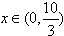时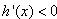，，h（x）是减函数当
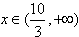时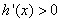，，h（x）是增函数∵
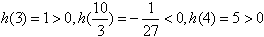
∴方程
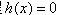在区间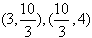内分别有惟一实数根，而在区间
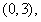
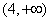内没有实数根所以存在惟一的自然数
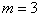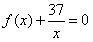，使得方程在区间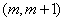内有且只有两个不同的实数根。
练习册系列答案
阅读快车系列答案
相关题目