题目内容
已知函数f（x）=1-
（x＞0），若存在实数a，b（a＜b），使y=f（x）的定义域为（a，b）时，值域为（ma，mb），则实数m的取值范围是________．
分析：由单调性的定义可得函数单调递增，故可得则
，即故
，由基本不等式可得
＞2，从而可得答案．解答：由题意，设0＜x1＜x2，则f（x1）-f（x2）
=（1-
）-（1-
）=-=
＜0，故函数f（x）=1-（x＞0）单调递增，若存在实数a，b（a＜b），使y=f（x）的定义域为（a，b）时，值域为（ma，mb），
则
，即
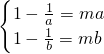，解得，由基本不等式可得1=
≥
，解＞2，（a＜b取不到等号），故m=
∈（0，
）故答案为：
点评：本题考查函数的值域，涉及函数的单调性和基本不等式，属中档题．
练习册系列答案
相关题目
已知函数f（x）=
，g（x）=1+
，若f（x）＞g（x），则实数x的取值范围是（ ）
| 1 |
| |x| |
| x+|x| |
| 2 |
| A、（-∞，-1）∪（0，1） | ||||
B、(-∞，-1)∪(0，
| ||||
C、(-1，0)∪(
| ||||
D、(-1，0)∪(0，
|