题目内容
在正方体ABCD－A1B1C1D1中，E、F分别是BB1、CD的中点，设AA1＝2，求三棱锥F－A1ED1的体积．
解：如图，连接AE，容易证明AE⊥D1F.
又∵A1D1⊥AE，
∴AE⊥平面A1FD1.
∵A1D1∥AD，A1D1∥平面ABCD，
设平面A1FD1∩平面ABCD＝FG，
则A1D1∥FG且G为AB的中点，
∴AE⊥平面A1GFD1，AE⊥A1G，
设垂足为点H，则EH即为点E到平面A1FD1的距离，
∵A1A＝2，∴AE＝
，AH＝
，∴EH＝
.
又∵S△A1FD1＝
S▱A1GFD1＝，
∴VF－A1ED1＝
××＝1，
故三棱锥F－A1ED1的体积为1.
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
在正方体ABCD-A1B1C1D1中，E是棱A1B1的中点，则A1B与D1E所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在正方体ABCD-A1B1C1D1中，AB与平面A1BC1所成角的正弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
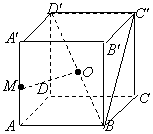
（本小题满分12分）
在正方体ABCD－A′B′C′D′中，点M是棱AA′的中点，点O是对角线BD′的中点.
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；
（Ⅱ）求二面角M－BC′－B′的大小；
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；
（Ⅰ）求证：OM为异面直线AA′和BD′的公垂线；