题目内容
设函数f(x)=|2x-1|+|2x-3|,x∈R
(Ⅰ)解不等式f(x)≤5;
(Ⅱ)若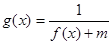 的定义域为R,求实数m的取值范围.
的定义域为R,求实数m的取值范围.
【答案】
(Ⅰ) 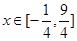 ;(Ⅱ)
;(Ⅱ) 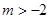
【解析】
试题分析:(Ⅰ)解绝对值不等式的关键是去绝对号,有多个绝对号的的不等式,利用零点分段法,分为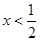 或
或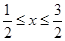 或
或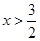 三种情况,在自变量的不同范围内分别解不等式,再取并集;(Ⅱ)等价于不等式
三种情况,在自变量的不同范围内分别解不等式,再取并集;(Ⅱ)等价于不等式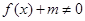 在R内恒成立,亦等价于方程
在R内恒成立,亦等价于方程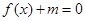 在R内无解,只需
在R内无解,只需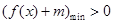 即可,从而得关于
即可,从而得关于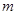 的不等式,进而的
的不等式,进而的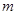 的取值范围.
的取值范围.
试题解析:(Ⅰ) 原不等式等价于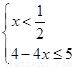 或
或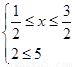 或
或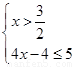 ,解得
,解得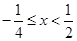 ,或
,或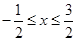 ,或
,或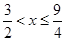 ,所以不等式的解集为
,所以不等式的解集为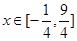 .
.
(Ⅱ) 若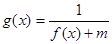 的定义域为R,则
的定义域为R,则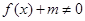 恒成立,即
恒成立,即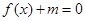 在R上无解,又
在R上无解,又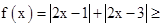
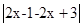
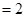 ,所以
,所以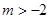 .
.
考点:1、绝对值不等式的解法;2、函数的定义域.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
设函数f(x)=2
,对于给定的正数K,定义函数fK(x)=
若对于函数f(x)=2
定义域内的任意 x,恒有fK(x)=f(x),则( )
| -x2+x+2 |
|
| -x2+x+2 |
A、K的最大值为2
| ||
B、K的最小值为2
| ||
| C、K的最大值为1 | ||
| D、K的最小值为1 |