题目内容
已知两定点 ,动点P满足
,动点P满足 ,由点P向x轴作垂线PQ,垂足为Q,点M满足
,由点P向x轴作垂线PQ,垂足为Q,点M满足 ,点M的轨迹为C.
,点M的轨迹为C.
(I)求曲线C的方程;
(II)若线段AB是曲线C的一条动弦,且|AB|=2,求坐标原点O到动弦AB距离的最大值.
解:(Ⅰ)设动点P(x0,y0),则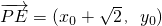 ,
,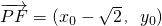 .
.
∵动点P满足 ,∴
,∴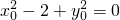 ,化为
,化为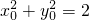
即动点P的轨迹方程为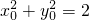 .
.
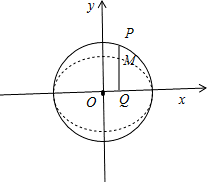
设动点M(x,y),则Q(x,0),如图所示,
∵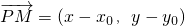 ,
,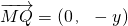 ,
, ,
,
∴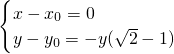 ,化为
,化为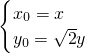 ,
,
代入动点P的轨迹方程得x2+2y2=2,即曲线C的方程为 .
.
(Ⅱ)当直线AB的斜率不存在时,∵|AB|=2=短轴长,∴直线AB经过原点,此时原点到直线的距离=0;
当直线AB的斜率存在时,设直线AB的方程为y=kx+t,
联立 ,消去y得(1+2k2)x2+4ktx+2t2-2=0,
,消去y得(1+2k2)x2+4ktx+2t2-2=0,
∵直线与椭圆有两个交点,∴△=16k2t2-4(1+2k2)(2t2-2)>0,化为t2<1+2k2.(*)
∴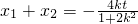 ,
,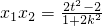 ,
,
∴|AB|=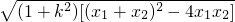 ,
,
∴22=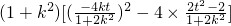 ,
,
化为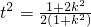 .(**)
.(**)
原点O到直线AB的距离d=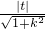 ,∴
,∴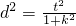 ,
,
把(**)代入上式得 =
=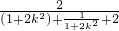
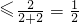 ,当且仅当
,当且仅当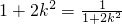 ,即k2=0,k=0时取等号.
,即k2=0,k=0时取等号.
此时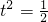 ,满足(*)式.
,满足(*)式.
∴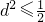 ,∴
,∴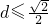 ,即原点O到直线AB的最大距离d=
,即原点O到直线AB的最大距离d= .
.
综上可知:坐标原点O到动弦AB距离的最大值是 .
.
分析:(Ⅰ)先求出动点P的轨迹方程,再根据已知条件用点M的坐标表示点P,使用“代点法”即可得出;
(Ⅱ)先对直线BA的斜率讨论,把直线AB的方程与椭圆的方程联立,利用根与系数的关系、弦长公式、点到直线的距离公式、基本不等式的性质即可得出.
点评:熟练掌握直线与椭圆相交问题的解题模式、根与系数的关系、弦长公式、点到直线的距离公式、基本不等式的性质、“代点法”是解题的关键.
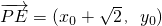 ,
,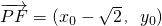 .
.
∵动点P满足
 ,∴
,∴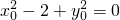 ,化为
,化为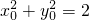
即动点P的轨迹方程为
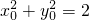 .
.设动点M(x,y),则Q(x,0),如图所示,
∵
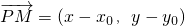 ,
,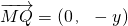 ,
, ,
,∴
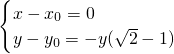 ,化为
,化为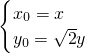 ,
,代入动点P的轨迹方程得x2+2y2=2,即曲线C的方程为
 .
.(Ⅱ)当直线AB的斜率不存在时,∵|AB|=2=短轴长,∴直线AB经过原点,此时原点到直线的距离=0;
当直线AB的斜率存在时,设直线AB的方程为y=kx+t,
联立
 ,消去y得(1+2k2)x2+4ktx+2t2-2=0,
,消去y得(1+2k2)x2+4ktx+2t2-2=0,∵直线与椭圆有两个交点,∴△=16k2t2-4(1+2k2)(2t2-2)>0,化为t2<1+2k2.(*)
∴
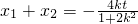 ,
,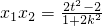 ,
,∴|AB|=
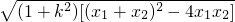 ,
,∴22=
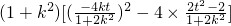 ,
,化为
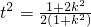 .(**)
.(**)原点O到直线AB的距离d=
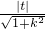 ,∴
,∴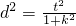 ,
,把(**)代入上式得
 =
=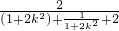
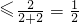 ,当且仅当
,当且仅当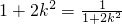 ,即k2=0,k=0时取等号.
,即k2=0,k=0时取等号.此时
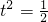 ,满足(*)式.
,满足(*)式.∴
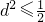 ,∴
,∴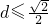 ,即原点O到直线AB的最大距离d=
,即原点O到直线AB的最大距离d= .
.综上可知:坐标原点O到动弦AB距离的最大值是
 .
.分析:(Ⅰ)先求出动点P的轨迹方程,再根据已知条件用点M的坐标表示点P,使用“代点法”即可得出;
(Ⅱ)先对直线BA的斜率讨论,把直线AB的方程与椭圆的方程联立,利用根与系数的关系、弦长公式、点到直线的距离公式、基本不等式的性质即可得出.
点评:熟练掌握直线与椭圆相交问题的解题模式、根与系数的关系、弦长公式、点到直线的距离公式、基本不等式的性质、“代点法”是解题的关键.

练习册系列答案
相关题目
 ,动点P满足
,动点P满足 ,由点P向x轴作垂线PQ,垂足为Q,点M满足
,由点P向x轴作垂线PQ,垂足为Q,点M满足 ,点M的轨迹为C.
,点M的轨迹为C. ,动点P满足
,动点P满足 ,由点P向x轴作垂线PQ,垂足为Q,点M满足
,由点P向x轴作垂线PQ,垂足为Q,点M满足 ,点M的轨迹为C.
,点M的轨迹为C.