题目内容

已知sina+sinB=
1
4
，cosa+cosB=
1
3
，求tg（a+B）的值．
解法一：由已知得
sinα+sinβ=2sin
α+β
2
cos
α-β
2
=
1
4
，
cosα+cosβ=2cos
α+β
2
cos
α-β
2
=
1
3
，
两式相除得
tan
α+β
2
=
2tan
α+β
2
1-tan2
α+β
2

=
2×
3
4
1-(
3
4
)2
=
24
7
练习册系列答案
相关题目
在△ABC中，已知tan
C
2
=sin（A+B），给出以下四个论断：
①tanA×cotB=1②1＜sinA+sinB≤
2

③sin2A+cos2B=1    ④sin2A+sin2B+sin2C=2
其中一定正确的是
 
（填上所有正确论断的序号）．
在△ABC中，内角A，B，C的对边分别为a，b，c，已知sinA=sin（A-B）+sinC．
（1）求角B的大小；
（2）若b2=ac，判断△ABC的形状；
（3）求证：
b•sin(C-
π
6
)
(2c-a)•cosB
为定值．

 [番茄花园1] （本题满分）在△ABC中，角A，B，C所对的边分别为a,b,c,设S为△ABC的面积，满足。

（Ⅰ）求角C的大小；

（Ⅱ）求的最大值。

 (Ⅰ)解：由题意可知

absinC=,2abcosC.

所以tanC=.

因为0<C<，

所以C=.

（Ⅱ)解：由已知sinA+sinB=sinA+sin(-C-A)=sinA+sin(-A)

                        =sinA+cosA+sinA=sin(A+)≤.

当△ABC为正三角形时取等号，

所以sinA+sinB的最大值是.

 

 

 [番茄花园1]1.

在△ABC中，内角A，B，C的对边分别为a，b，c，已知sinA=sin（A-B）+sinC．
（1）求角B的大小；
（2）若b2=ac，判断△ABC的形状；
（3）求证：
b•sin(C-
π
6
)
(2c-a)•cosB
为定值．

已知sina＝,aÎ(,p)，cosb＝－，b是第三象限的角.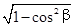

⑴ 求cos(a－b)的值；

⑵ 求sin(a＋b)的值；

⑶ 求tan2a的值.

【解析】第一问中∵ aÎ(,p),∴ cosa＝－＝－,  ∵ b是第三象限的角，

∴ sinb＝－＝－,     

cos(a－b)＝cosa·cosb＋sina·sinb ＝(－)×(－)＋×(－)＝－ 

⑵ 中sin(a＋b)＝sina·cosb＋cosa·sinb       ＝×(－)＋(－)×(－)＝ ⑶ 利用二倍角的正切公式得到。∵tana＝＝－ ∴tan2a＝ ＝＝－ 

解∵ aÎ(,p),∴ cosa＝－＝－,         …………1分

∵ b是第三象限的角，∴ sinb＝－＝－,        ………2分

⑴ cos(a－b)＝cosa·cosb＋sina·sinb          …………3分

＝(－)×(－)＋×(－)＝－          ………………5分

⑵ sin(a＋b)＝sina·cosb＋cosa·sinb          ……………………6分

＝×(－)＋(－)×(－)＝           …………………8分

⑶ ∵tana＝＝－             …………………9分

∴tan2a＝             ………………10分

＝＝－

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网