题目内容
已知椭圆C: (a>b>0)的右焦点为F(2,0),且过点P(2,
(a>b>0)的右焦点为F(2,0),且过点P(2, ).直线l过点F且交椭圆C于A、B两点.
).直线l过点F且交椭圆C于A、B两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若线段AB的垂直平分线与x轴的交点为M(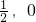 ),求直线l的方程.
),求直线l的方程.
解:(Ⅰ)由题意得, ,解得a2=8,b2=4,
,解得a2=8,b2=4,
所以椭圆C的方程为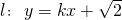 ;
;
(Ⅱ)当直线l斜率不存在时,不符合题意,
当斜率存在时设直线l的方程为y=k(x-2),A(x1,y1)、B(x2,y2),AB的中点为N(x0,y0),
由 得(1+2k2)x2-8k2x+8k2-8=0,
得(1+2k2)x2-8k2x+8k2-8=0,
因为△=64k4-4(1+2k2)(8k2-8)=32(k2+1)>0,
所以 ,
,
所以 ,
, ,
,
因为线段AB的垂直平分线过点M(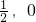 ),
),
所以kMN•k=-1,即 ,
,
所以 ,
,
解得,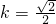 ,
,
所以直线l的方程为 或
或 .
.
分析:(Ⅰ)根据题意可得 ,解出即可;
,解出即可;
(Ⅱ)易知直线l存在斜率,设直线l的方程为y=k(x-2),A(x1,y1)、B(x2,y2),AB的中点为N(x0,y0),联立直线方程与椭圆方程消掉y得x的二次方程,由韦达定理及中点坐标公式可用k表示出AB中点N的坐标,由题意得kMN•k=-1,即 ,把x0,y0用k表示出来即得关于k的方程,解出方程然后运用点斜式即可求得l的方程;
,把x0,y0用k表示出来即得关于k的方程,解出方程然后运用点斜式即可求得l的方程;
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,韦达定理、判别式是解决该类题目的常用知识,正确挖掘“线段AB的垂直平分线与x轴的交点为M”所含信息是解决(Ⅱ)问的关键.
 ,解得a2=8,b2=4,
,解得a2=8,b2=4,所以椭圆C的方程为
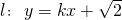 ;
;(Ⅱ)当直线l斜率不存在时,不符合题意,
当斜率存在时设直线l的方程为y=k(x-2),A(x1,y1)、B(x2,y2),AB的中点为N(x0,y0),
由
 得(1+2k2)x2-8k2x+8k2-8=0,
得(1+2k2)x2-8k2x+8k2-8=0,因为△=64k4-4(1+2k2)(8k2-8)=32(k2+1)>0,
所以
 ,
,所以
 ,
, ,
,因为线段AB的垂直平分线过点M(
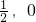 ),
),所以kMN•k=-1,即
 ,
,所以
 ,
,解得,
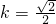 ,
,所以直线l的方程为
 或
或 .
.分析:(Ⅰ)根据题意可得
 ,解出即可;
,解出即可;(Ⅱ)易知直线l存在斜率,设直线l的方程为y=k(x-2),A(x1,y1)、B(x2,y2),AB的中点为N(x0,y0),联立直线方程与椭圆方程消掉y得x的二次方程,由韦达定理及中点坐标公式可用k表示出AB中点N的坐标,由题意得kMN•k=-1,即
 ,把x0,y0用k表示出来即得关于k的方程,解出方程然后运用点斜式即可求得l的方程;
,把x0,y0用k表示出来即得关于k的方程,解出方程然后运用点斜式即可求得l的方程;点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,韦达定理、判别式是解决该类题目的常用知识,正确挖掘“线段AB的垂直平分线与x轴的交点为M”所含信息是解决(Ⅱ)问的关键.

练习册系列答案
相关题目
 (a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),离心率为
(a>b>0)的左、右焦点分别为F1(-1,0)、F2(1,0),离心率为 .
. (O为坐标原点),求△AOB的面积;
(O为坐标原点),求△AOB的面积;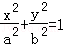 (a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点
(a>b>0)的两个焦点分别为F1(﹣1,0),F2(1,0),且椭圆C经过点 .
. ,求点Q的轨迹方程.
,求点Q的轨迹方程. (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为 ,直线y=k(x-1)与椭圆C交于不同的两点M、N.
,直线y=k(x-1)与椭圆C交于不同的两点M、N. 时,求k的值.
时,求k的值. +
+ =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C(
与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心为I,且IG∥F1F2。⑴求椭圆C的方程。⑵若直线L:y=kx+m(k≠0)与椭圆C交于不同两点A,B且线段AB的垂直平分线过定点C( ,0)求实数k的取值范围。
,0)求实数k的取值范围。 (a>b>0)的离心率为
(a>b>0)的离心率为 ,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线与椭圆C相交于A、B两点,若 。则
。则 ( )
( )  (D)
(D)