Question

双曲线的左、可焦点分别为F₁、F₂，O为坐标原点，点A在双曲线的右支下，点B在双曲线左准线上，

   （1）求双曲线的离心率e；

   （2）若此双曲线过C（2，），求双曲线的方程；

   （3）在（2）的条件下，D₁、D₂分别是双曲线的虚轴端点（D₂在y轴正半轴上），过D₁的直线l交双曲线M、N，的方程.

Answer 1

解：（1）四边形F₂ABO是平行四边形

又由

∴四边 形F₂ABO是菱形.

∴

由双曲线定义得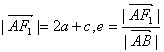

（2）

，双曲线方程为

把点C代入有

∴双曲线方程

（3）D₁（0，－3），D₂（0，3），设l的方程为

则由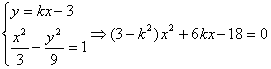

因为与双曲线有两个交点，

故所求直线l方程为