题目内容
已知二次函数f(x)=ax2-4x+c+1的值域是[1,+∞),则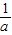 +
+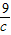 的最小值是 .
的最小值是 .
【答案】分析:由已知可得a>0且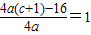 ,然后利用基本不等式即可求解最值
,然后利用基本不等式即可求解最值
解答:解:∵f(x)=ax2-4x+c+1的值域是[1,+∞),
∴a>0且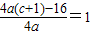 即ac=4
即ac=4
∴c>0
∴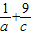
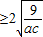 =3
=3
当且仅当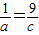 且ac=4,则a=
且ac=4,则a=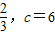 时取等号
时取等号
∴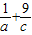 的最小值为3
的最小值为3
故答案为:3
点评:本题主要考查了二次函数的性质的应用,基本不等式求解函数的最值等知识的综合应用.
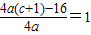 ,然后利用基本不等式即可求解最值
,然后利用基本不等式即可求解最值解答:解:∵f(x)=ax2-4x+c+1的值域是[1,+∞),
∴a>0且
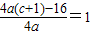 即ac=4
即ac=4∴c>0
∴
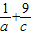
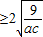 =3
=3当且仅当
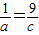 且ac=4,则a=
且ac=4,则a=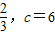 时取等号
时取等号∴
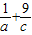 的最小值为3
的最小值为3故答案为:3
点评:本题主要考查了二次函数的性质的应用,基本不等式求解函数的最值等知识的综合应用.

练习册系列答案
相关题目