题目内容
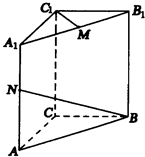 如图,直三棱柱ABC-A1B1C1底面△ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,M,N分别是A1B1,AA1的中点.
如图,直三棱柱ABC-A1B1C1底面△ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,M,N分别是A1B1,AA1的中点.(1)求证NB⊥C1M;
(2)求cos<
| BA1 |
| CB1 |
(3)求平面BNC与平面BCC1B1所成的角的余弦值.
分析:(I)根据题意,分别以CA、CB、CC1所在直线为x、y、z轴建立空间坐标系,如图所示.从而算出
、
的坐标,得到数量积
•
=0.从而可得
⊥
,即NB⊥C1M;
(II)由(I)的坐标系,得到向量
、
的坐标,利用空间向量的夹角公式加以计算,即可得到cos<
,
>的值;
(III)取CC1的中点H,连NH、NC.利用面面垂直的定义与性质,结合题意证出BC⊥平面AA1C1C,从而BC⊥CN,结合BC⊥C1C得∠NCH是平面BNC与平面BCC1B1所成二面角的平面角.Rt△NCH中,利用题中数据算出∠NCH大小,从而得到平面BNC与平面BCC1B1所成的角的余弦值.
| BN |
| C1M |
| BN |
| C1M |
| BN |
| C1M |
(II)由(I)的坐标系,得到向量
| BA1 |
| CB1 |
| BA1 |
| CB1 |
(III)取CC1的中点H,连NH、NC.利用面面垂直的定义与性质,结合题意证出BC⊥平面AA1C1C,从而BC⊥CN,结合BC⊥C1C得∠NCH是平面BNC与平面BCC1B1所成二面角的平面角.Rt△NCH中,利用题中数据算出∠NCH大小,从而得到平面BNC与平面BCC1B1所成的角的余弦值.
解答:解:( I )∵直三棱柱ABC-A1B1C1中,∠ACB=90°
∴CA、CB、CC1两两互相垂直,
因此,分别以CA、CB、CC1所在直线为x、y、z轴建立空间坐标系,如图所示.
则A(1,0,0),B(0,1,0),A1 (1,0,2),B1 ( 0,1,2),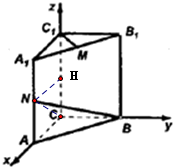
C1(0,0,2),M(
,
,2),N(1,0,1),
∴
=(1,-1,1),
=(
,
,0),
∴
•
=1×
+(-1)×
+1×0=0,
可得
⊥
,即NB⊥C1M;
(II)由(I)得:
=(1,-1,2),
=( 0,1,2).
∴cos<
,
>=
=
=
即cos<
,
>的值为
;
(III)取CC1的中点H,连线NH、NC,则NH∥CA
∵∠BCA=90°,直三棱柱ABC-A1B1C1中,∠BCA是A-CC1-B的平面角
∴平面AA1C1C⊥平面BB1C1C,
结合BC⊥CC1可得BC⊥平面AA1C1C,得BC⊥CN
∴∠NCH就是平面BNC与平面BCC1B1所成二面角的平面角
Rt△NCH中,NH=1,CH=
CC1=1,所以∠NCH=45°
因此,平面BNC与平面BCC1B1所成的角的余弦值等于cos45°=
.
∴CA、CB、CC1两两互相垂直,
因此,分别以CA、CB、CC1所在直线为x、y、z轴建立空间坐标系,如图所示.
则A(1,0,0),B(0,1,0),A1 (1,0,2),B1 ( 0,1,2),

C1(0,0,2),M(
| 1 |
| 2 |
| 1 |
| 2 |
∴
| BN |
| C1M |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| BN |
| C1M |
| 1 |
| 2 |
| 1 |
| 2 |
可得
| BN |
| C1M |
(II)由(I)得:
| BA1 |
| CB1 |
∴cos<
| BA1 |
| CB1 |
| ||||
|
| 1×0+(-1)×1+2×2 | ||||
|
| ||
| 10 |
即cos<
| BA1 |
| CB1 |
| ||
| 10 |
(III)取CC1的中点H,连线NH、NC,则NH∥CA
∵∠BCA=90°,直三棱柱ABC-A1B1C1中,∠BCA是A-CC1-B的平面角
∴平面AA1C1C⊥平面BB1C1C,
结合BC⊥CC1可得BC⊥平面AA1C1C,得BC⊥CN
∴∠NCH就是平面BNC与平面BCC1B1所成二面角的平面角
Rt△NCH中,NH=1,CH=
| 1 |
| 2 |
因此,平面BNC与平面BCC1B1所成的角的余弦值等于cos45°=
| ||
| 2 |
点评:本题在直三棱柱中求线线垂直、求异面直线所成角并求二面角的大小.着重考查了直棱柱的性质、利用空间坐标系研究线线角和面面角等知识,属于中档题.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.