题目内容
已知椭圆| x2 |
| 2 |
| y2 |
| 4 |
| 2 |
(Ⅰ)求证:直线BC的斜率为定值,并求这个定值;
(Ⅱ)求三角形ABC的面积最大值.
分析:(Ⅰ)由题意得A(1,
),设AB的斜率为k,则AC的斜率为-k,所以
,由此可知直线BC的斜率为定值,并且能够求出这个定值.
(Ⅱ)设BC方程为y=
x+m,由
得4x2+2
mx+m2-4=0,得|BC|=
.
,A到BC的距离为d=
;由此可得答案.
| 2 |
|
(Ⅱ)设BC方程为y=
| 2 |
|
| 2 |
| 3 |
4-
|
| |m| | ||
|
解答:解:(Ⅰ)由题意得A(1,
),设AB的斜率为k,则AC的斜率为-k,
所以
,代入得x1+x2=
,又∵x1=1,∴xB=
;同理xC=
.kBC=
=
=
为定值.(8分)
(Ⅱ)设BC方程为y=
x+m,由
得4x2+2
mx+m2-4=0,得|BC|=
.
,A到BC的距离为d=
;
所以S△=
|BC|•d=
|m|
=
=
≤
.
当m2=8-m2时,即m2=4时“=”成立,此时△>0成立.(14分)
| 2 |
所以
|
2k2-2
| ||
| 2+k2 |
k2-2
| ||
| k2+2 |
k2+2
| ||
| k2+2 |
| yB-yC |
| xB-xC |
kxB-k+
| ||||
| xB-xC |
| 2 |
(Ⅱ)设BC方程为y=
| 2 |
|
| 2 |
| 3 |
4-
|
| |m| | ||
|
所以S△=
| 1 |
| 2 |
| 1 |
| 2 |
4-
|
| 1 |
| 2 |
m2(4-
|
| ||
| 4 |
| m2(8-m2) |
| 2 |
当m2=8-m2时,即m2=4时“=”成立,此时△>0成立.(14分)
点评:圆锥曲线的综合大题,主要考查解析几何的有关知识,以及分析问题与解决问题的能力.基本上是每年一道大题.主要是以直线与圆锥曲线的位置关系的形式出现.考查学生基本方法和基本运算,值得引起重视的一个现象是字母多的运算,同时要注意其与平面向量以及导数的知识的综合命题.

练习册系列答案
相关题目
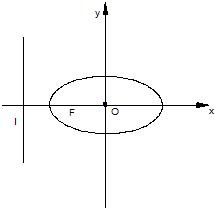 已知椭圆
已知椭圆 已知椭圆
已知椭圆