题目内容
如图,正四棱柱ABCD-A1B1C1D1中,底面边长为22,侧棱长为4.E,F分别为棱AB,BC的中点,EF∩BD=G.(1)求证:平面BEF⊥平面BDD1B1;
(2)求点D1到平面B1EF的距离d;
(3)求三棱锥B1-EFD1的体积V.
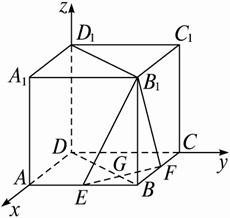
思路分析:先建立直角坐标系,再求出各点的坐标,用向量法求解,证明即可.
解:(1)如图,以D为原点,DA、DC、DD1分别为x,y,z轴建立直角坐标系,依题意,有

A(![]() ,0,0),C(0,
,0,0),C(0,![]() ,0),E(
,0),E(![]() ,
,![]() ,0),F(
,0),F(![]() ,
,![]() ,0),B1(
,0),B1(![]() ,
,![]() ,4),D1(0,0,4).
,4),D1(0,0,4).
设平面B1EF的法向量为n=(x,y,z),
由n⊥![]() ,n⊥
,n⊥![]() ,
,![]() =(0,
=(0,![]() ,-4),
,-4),![]() =(
=(![]() ,
,![]() ,0),
,0),
得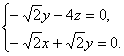 ∴x∶y∶z=1∶1∶(
∴x∶y∶z=1∶1∶(![]() ),n=(1,1,
),n=(1,1,![]() ).
).
又平面BDD1B1的法向量![]() =(
=(![]() ,0),
,0),
∵n·![]() =1×(
=1×(![]() )+1×(
)+1×(![]() )+(
)+(![]() )×0=0,
)×0=0,
∴平面B1EF⊥平面BDD1B1.
(2)∵![]() =(
=(![]() ,0),∴平面B1EF的法向量n=(1,1,
,0),∴平面B1EF的法向量n=(1,1,![]() ).
).
∴D1到平面B1EF的距离d=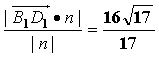 .
.
(3)∵![]() =(0,
=(0,![]() ,-4),
,-4),![]() =(
=(![]() ,0 ,-4),
,0 ,-4),
∴cos〈![]() ,
,![]() 〉=
〉=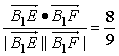 .
.
∴sin〈![]() ,
,![]() 〉=
〉=![]() .
.
∴S△BEF=![]() |
|![]() |·|
|·|![]() |sin〈
|sin〈![]() ,
,![]() 〉=
〉=![]() ×18×
×18×![]() ,
,
![]() .
.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
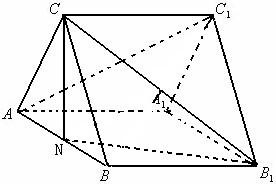 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
