题目内容
设f（x）是以3为周期的周期函数，且x∈（0，3]时f（x）=lgx，N是y=f（x）图象上的动点，
=(2，10），则以M点的轨迹为图象的函数在（1，4]上的解析式为（ ）
| MN |
| A．g（x）=lg（x-1）-10，x∈（1，4] | B．g（x）=lg（x-1）+10，x∈（1，4] |
| C．g（x）=lg（x-5）+10，x∈（1，4] | D．g（x）=lg（x+2）-10，x∈（1，4] |
设M（x，y），且1＜x≤4，∵
=(2，10)，
∴N=（x+2，y+10），∴3＜x+2≤6，
∵f（x）是以3为周期的周期函数，∴f（x）=f（x-3）
∵x∈（0，3]时f（x）=lgx，N是y=f（x）图象上的动点，
∴f（x+2）=f（x-1），∴y+10=lg（x-1），则y=lg（x-1）-10，
所以所求的解析式：g（x）=lg（x-1）-10，x∈（1，4]．
故选A．
| MN |
∴N=（x+2，y+10），∴3＜x+2≤6，
∵f（x）是以3为周期的周期函数，∴f（x）=f（x-3）
∵x∈（0，3]时f（x）=lgx，N是y=f（x）图象上的动点，
∴f（x+2）=f（x-1），∴y+10=lg（x-1），则y=lg（x-1）-10，
所以所求的解析式：g（x）=lg（x-1）-10，x∈（1，4]．
故选A．
练习册系列答案
53随堂测系列答案
相关题目
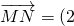，10），则以M点的轨迹为图象的函数在（1，4]上的解析式为
，10），则以M点的轨迹为图象的函数在（1，4]上的解析式为（ ）